Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
Please solve both questions explain me I would like to understand and compare my answers
![**Educational Content: Linear Algebra Problems**
---
**Problem 1: True/False Question**
Determine whether the following statement is true or false:
The matrix \( A = \begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \) is invertible.
**Explanation:**
A matrix is invertible if its determinant is non-zero. Calculate the determinant of matrix \( A \) to see if it meets this condition.
---
**Problem 2: Vector Space and Kernel**
Find vectors that span the kernel of the matrix:
\[ A = \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3 \end{bmatrix} \]
**Explanation:**
To find the kernel of the matrix \( A \), solve the equation \( A\mathbf{x} = \mathbf{0} \), where \( \mathbf{x} \) is a vector. The solution set will provide the vectors that span the kernel.
---
This educational content is designed to facilitate understanding of matrix properties and vector spaces, foundational concepts in linear algebra.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F8cf9958e-dd38-41eb-b691-55a1e2252bf8%2Fa8abc021-d522-470e-8852-44456d66403a%2Fjjtu87a_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Educational Content: Linear Algebra Problems**
---
**Problem 1: True/False Question**
Determine whether the following statement is true or false:
The matrix \( A = \begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \) is invertible.
**Explanation:**
A matrix is invertible if its determinant is non-zero. Calculate the determinant of matrix \( A \) to see if it meets this condition.
---
**Problem 2: Vector Space and Kernel**
Find vectors that span the kernel of the matrix:
\[ A = \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3 \end{bmatrix} \]
**Explanation:**
To find the kernel of the matrix \( A \), solve the equation \( A\mathbf{x} = \mathbf{0} \), where \( \mathbf{x} \) is a vector. The solution set will provide the vectors that span the kernel.
---
This educational content is designed to facilitate understanding of matrix properties and vector spaces, foundational concepts in linear algebra.
Expert Solution
Step 1
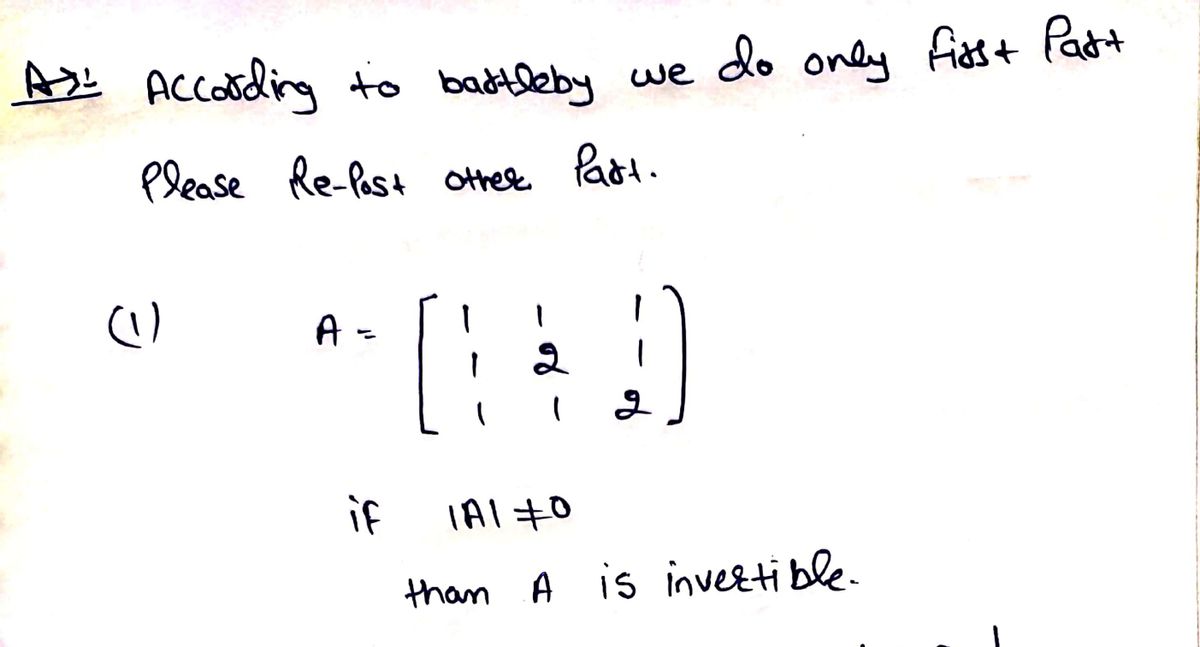
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education