### Question Given that \(\sec(\theta) = -\frac{\sqrt{5}}{2}\) and \(\theta\) is in Quadrant II, what is \(\tan(\theta)\)? Write your answer in exact form. Do not round. **Provide your answer below:** \[ \tan(\theta) = \boxed{\phantom{answer}} \] **Options:** - [Feedback] - [More Instruction] **Contact Attribution** --- **Explanation:** To find \(\tan(\theta)\), recall that the identity relating secant and cosine is \(\sec(\theta) = \frac{1}{\cos(\theta)}\). Since \(\sec(\theta) = -\frac{\sqrt{5}}{2}\), it follows that \(\cos(\theta) = -\frac{2}{\sqrt{5}}\). In Quadrant II, sine is positive and cosine is negative. Using the Pythagorean identity \(\sin^2(\theta) + \cos^2(\theta) = 1\), solve for \(\sin(\theta)\): 1. First, square \(\cos(\theta)\): \[ \cos^2(\theta) = \left(-\frac{2}{\sqrt{5}}\right)^2 = \frac{4}{5} \] 2. Substitute into the Pythagorean identity: \[ \sin^2(\theta) + \frac{4}{5} = 1 \] 3. Solve for \(\sin^2(\theta)\): \[ \sin^2(\theta) = 1 - \frac{4}{5} = \frac{1}{5} \] 4. Since \(\theta\) is in Quadrant II, \(\sin(\theta)\) is positive: \[ \sin(\theta) = \frac{1}{\sqrt{5}} \] 5. Finally, calculate \(\tan(\theta)\) as \(\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\): \[ \tan(\theta) = \frac{\frac{1}{\sqrt{5}}}{-\frac{2}{\sqrt{5}}} = -\frac{1}{2} \] Thus, the exact value of \(\tan(\theta)\)
### Question Given that \(\sec(\theta) = -\frac{\sqrt{5}}{2}\) and \(\theta\) is in Quadrant II, what is \(\tan(\theta)\)? Write your answer in exact form. Do not round. **Provide your answer below:** \[ \tan(\theta) = \boxed{\phantom{answer}} \] **Options:** - [Feedback] - [More Instruction] **Contact Attribution** --- **Explanation:** To find \(\tan(\theta)\), recall that the identity relating secant and cosine is \(\sec(\theta) = \frac{1}{\cos(\theta)}\). Since \(\sec(\theta) = -\frac{\sqrt{5}}{2}\), it follows that \(\cos(\theta) = -\frac{2}{\sqrt{5}}\). In Quadrant II, sine is positive and cosine is negative. Using the Pythagorean identity \(\sin^2(\theta) + \cos^2(\theta) = 1\), solve for \(\sin(\theta)\): 1. First, square \(\cos(\theta)\): \[ \cos^2(\theta) = \left(-\frac{2}{\sqrt{5}}\right)^2 = \frac{4}{5} \] 2. Substitute into the Pythagorean identity: \[ \sin^2(\theta) + \frac{4}{5} = 1 \] 3. Solve for \(\sin^2(\theta)\): \[ \sin^2(\theta) = 1 - \frac{4}{5} = \frac{1}{5} \] 4. Since \(\theta\) is in Quadrant II, \(\sin(\theta)\) is positive: \[ \sin(\theta) = \frac{1}{\sqrt{5}} \] 5. Finally, calculate \(\tan(\theta)\) as \(\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\): \[ \tan(\theta) = \frac{\frac{1}{\sqrt{5}}}{-\frac{2}{\sqrt{5}}} = -\frac{1}{2} \] Thus, the exact value of \(\tan(\theta)\)
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
![### Question
Given that \(\sec(\theta) = -\frac{\sqrt{5}}{2}\) and \(\theta\) is in Quadrant II, what is \(\tan(\theta)\)? Write your answer in exact form. Do not round.
**Provide your answer below:**
\[
\tan(\theta) = \boxed{\phantom{answer}}
\]
**Options:**
- [Feedback]
- [More Instruction]
**Contact Attribution**
---
**Explanation:**
To find \(\tan(\theta)\), recall that the identity relating secant and cosine is \(\sec(\theta) = \frac{1}{\cos(\theta)}\). Since \(\sec(\theta) = -\frac{\sqrt{5}}{2}\), it follows that \(\cos(\theta) = -\frac{2}{\sqrt{5}}\).
In Quadrant II, sine is positive and cosine is negative. Using the Pythagorean identity \(\sin^2(\theta) + \cos^2(\theta) = 1\), solve for \(\sin(\theta)\):
1. First, square \(\cos(\theta)\):
\[ \cos^2(\theta) = \left(-\frac{2}{\sqrt{5}}\right)^2 = \frac{4}{5} \]
2. Substitute into the Pythagorean identity:
\[ \sin^2(\theta) + \frac{4}{5} = 1 \]
3. Solve for \(\sin^2(\theta)\):
\[ \sin^2(\theta) = 1 - \frac{4}{5} = \frac{1}{5} \]
4. Since \(\theta\) is in Quadrant II, \(\sin(\theta)\) is positive:
\[ \sin(\theta) = \frac{1}{\sqrt{5}} \]
5. Finally, calculate \(\tan(\theta)\) as \(\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\):
\[ \tan(\theta) = \frac{\frac{1}{\sqrt{5}}}{-\frac{2}{\sqrt{5}}} = -\frac{1}{2} \]
Thus, the exact value of \(\tan(\theta)\)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2e8c8f34-aa16-4232-a0f4-4bb6690b9b9d%2Fbfc05f57-eff2-482a-ae48-e83350599f4a%2F9jxt7b7.jpeg&w=3840&q=75)
Transcribed Image Text:### Question
Given that \(\sec(\theta) = -\frac{\sqrt{5}}{2}\) and \(\theta\) is in Quadrant II, what is \(\tan(\theta)\)? Write your answer in exact form. Do not round.
**Provide your answer below:**
\[
\tan(\theta) = \boxed{\phantom{answer}}
\]
**Options:**
- [Feedback]
- [More Instruction]
**Contact Attribution**
---
**Explanation:**
To find \(\tan(\theta)\), recall that the identity relating secant and cosine is \(\sec(\theta) = \frac{1}{\cos(\theta)}\). Since \(\sec(\theta) = -\frac{\sqrt{5}}{2}\), it follows that \(\cos(\theta) = -\frac{2}{\sqrt{5}}\).
In Quadrant II, sine is positive and cosine is negative. Using the Pythagorean identity \(\sin^2(\theta) + \cos^2(\theta) = 1\), solve for \(\sin(\theta)\):
1. First, square \(\cos(\theta)\):
\[ \cos^2(\theta) = \left(-\frac{2}{\sqrt{5}}\right)^2 = \frac{4}{5} \]
2. Substitute into the Pythagorean identity:
\[ \sin^2(\theta) + \frac{4}{5} = 1 \]
3. Solve for \(\sin^2(\theta)\):
\[ \sin^2(\theta) = 1 - \frac{4}{5} = \frac{1}{5} \]
4. Since \(\theta\) is in Quadrant II, \(\sin(\theta)\) is positive:
\[ \sin(\theta) = \frac{1}{\sqrt{5}} \]
5. Finally, calculate \(\tan(\theta)\) as \(\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\):
\[ \tan(\theta) = \frac{\frac{1}{\sqrt{5}}}{-\frac{2}{\sqrt{5}}} = -\frac{1}{2} \]
Thus, the exact value of \(\tan(\theta)\)
Expert Solution
Step 1
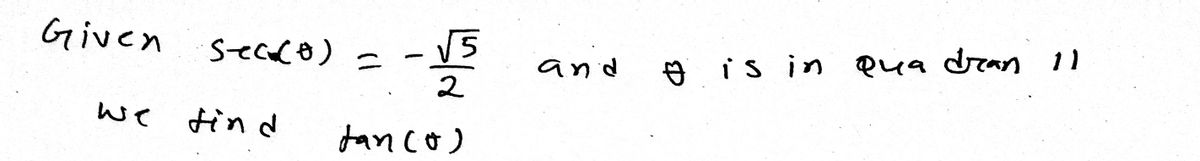
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning