Verify the identity.
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
100%
![**Verification of the Identity:**
\[
\frac{\cos(u) \sec(u)}{\tan(u)} = \cot(u)
\]
**Objective:** Use a Reciprocal Identity to rewrite the expression and then simplify.
Step-by-Step Solution:
1. Begin with the given expression:
\[
\frac{\cos(u) \sec(u)}{\tan(u)}
\]
2. Apply the Reciprocal Identity. Expand \(\tan(u)\) as \(\frac{\sin(u)}{\cos(u)}\):
\[
\frac{\cos(u) \sec(u)}{\frac{\sin(u)}{\cos(u)}}
\]
Red note with an "X" indicates an incorrect approach by rewriting the expression as \((\cos(u) \sec(u))(\tan(u))\). This approach is not correct.
3. Simplify the multiplication:
\[
= \cos(u) \cdot \sec(u) \cdot \frac{\cos(u)}{\sin(u)}
\]
4. Recognize that \(\sec(u) = \frac{1}{\cos(u)}\):
\[
= \cos(u) \cdot \frac{1}{\cos(u)} \cdot \frac{\cos(u)}{\sin(u)}
\]
5. Simplify the intermediate expression:
\[
= \cos(u) \cdot \frac{1}{\cos(u)} \cdot \frac{\cos(u)}{\sin(u)}
\]
So,
\[
= \cos(u) \cdot \frac{\cos(u)}{\cos(u)} \cdot \frac{1}{\sin(u)}
\]
6. Simplify \(\frac{\cos(u)}{\cos(u)}\) to 1:
\[
= 1 \cdot \frac{1}{\sin(u)}
\]
7. Thus, the expression simplifies to the cotangent function:
\[
= \cot(u) \quad \checkmark
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fbd285f6f-67ec-4ffa-8e9b-700f12fa780d%2F88907842-b445-40bd-8eff-c9ba14447494%2Fsdjp8b.jpeg&w=3840&q=75)
Transcribed Image Text:**Verification of the Identity:**
\[
\frac{\cos(u) \sec(u)}{\tan(u)} = \cot(u)
\]
**Objective:** Use a Reciprocal Identity to rewrite the expression and then simplify.
Step-by-Step Solution:
1. Begin with the given expression:
\[
\frac{\cos(u) \sec(u)}{\tan(u)}
\]
2. Apply the Reciprocal Identity. Expand \(\tan(u)\) as \(\frac{\sin(u)}{\cos(u)}\):
\[
\frac{\cos(u) \sec(u)}{\frac{\sin(u)}{\cos(u)}}
\]
Red note with an "X" indicates an incorrect approach by rewriting the expression as \((\cos(u) \sec(u))(\tan(u))\). This approach is not correct.
3. Simplify the multiplication:
\[
= \cos(u) \cdot \sec(u) \cdot \frac{\cos(u)}{\sin(u)}
\]
4. Recognize that \(\sec(u) = \frac{1}{\cos(u)}\):
\[
= \cos(u) \cdot \frac{1}{\cos(u)} \cdot \frac{\cos(u)}{\sin(u)}
\]
5. Simplify the intermediate expression:
\[
= \cos(u) \cdot \frac{1}{\cos(u)} \cdot \frac{\cos(u)}{\sin(u)}
\]
So,
\[
= \cos(u) \cdot \frac{\cos(u)}{\cos(u)} \cdot \frac{1}{\sin(u)}
\]
6. Simplify \(\frac{\cos(u)}{\cos(u)}\) to 1:
\[
= 1 \cdot \frac{1}{\sin(u)}
\]
7. Thus, the expression simplifies to the cotangent function:
\[
= \cot(u) \quad \checkmark
\]
![# Verifying Trigonometric Identities
## Verifying the Identity:
Given the identity:
\[ \frac{\sec(t) - \cos(t)}{\sec(t)} = \sin^2(t) \]
We aim to verify this identity using fundamental trigonometric identities.
## Step-by-Step Verification
### Step 1: Use a Reciprocal Identity
Firstly, we use the reciprocal identity for \(\sec(t)\):
\[ \sec(t) = \frac{1}{\cos(t)} \]
Rewrite the given expression in terms of cosine only:
\[ \frac{\sec(t) - \cos(t)}{\sec(t)} \]
Substitute the reciprocal identity \(\sec(t) = \frac{1}{\cos(t)}\):
\[ \frac{\frac{1}{\cos(t)} - \cos(t)}{\frac{1}{\cos(t)}} \]
### Step 2: Simplify the Expression
Factor out \(\frac{1}{\cos(t)}\):
\[ \left( \frac{1}{\cos(t)} \right) \left( \frac{1}{\cos(t)} - \cos(t) \right) \]
Combine the terms in the numerator:
\[ \frac{1}{\cos(t)} \left( \frac{1 - \cos^2(t)}{\cos(t)} \right) \]
Multiply out:
\[ = \frac{1 - \cos^2(t)}{\cos^2(t)} \]
### Step 3: Use a Pythagorean Identity
Recall the Pythagorean identity:
\[ \sin^2(t) + \cos^2(t) = 1 \]
So,
\[ 1 - \cos^2(t) = \sin^2(t) \]
Substitute \(\sin^2(t)\) into the expression:
\[ \frac{\sin^2(t)}{\cos^2(t)} \]
### Step 4: Simplify Further
Recognize that:
\[ \frac{\sin^2(t)}{\cos^2(t)} = \tan^2(t) \]
Since the given expression simplifies to \( \sin^2(t) \), the identity is verified:
\[ \boxed{\sin^2(t)} \]
By carefully substituting identities and simplifying step-by-step, we verify that:
\[ \frac{\sec(t) - \cos(t)}{\sec(t)}](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fbd285f6f-67ec-4ffa-8e9b-700f12fa780d%2F88907842-b445-40bd-8eff-c9ba14447494%2F1jeos8r.jpeg&w=3840&q=75)
Transcribed Image Text:# Verifying Trigonometric Identities
## Verifying the Identity:
Given the identity:
\[ \frac{\sec(t) - \cos(t)}{\sec(t)} = \sin^2(t) \]
We aim to verify this identity using fundamental trigonometric identities.
## Step-by-Step Verification
### Step 1: Use a Reciprocal Identity
Firstly, we use the reciprocal identity for \(\sec(t)\):
\[ \sec(t) = \frac{1}{\cos(t)} \]
Rewrite the given expression in terms of cosine only:
\[ \frac{\sec(t) - \cos(t)}{\sec(t)} \]
Substitute the reciprocal identity \(\sec(t) = \frac{1}{\cos(t)}\):
\[ \frac{\frac{1}{\cos(t)} - \cos(t)}{\frac{1}{\cos(t)}} \]
### Step 2: Simplify the Expression
Factor out \(\frac{1}{\cos(t)}\):
\[ \left( \frac{1}{\cos(t)} \right) \left( \frac{1}{\cos(t)} - \cos(t) \right) \]
Combine the terms in the numerator:
\[ \frac{1}{\cos(t)} \left( \frac{1 - \cos^2(t)}{\cos(t)} \right) \]
Multiply out:
\[ = \frac{1 - \cos^2(t)}{\cos^2(t)} \]
### Step 3: Use a Pythagorean Identity
Recall the Pythagorean identity:
\[ \sin^2(t) + \cos^2(t) = 1 \]
So,
\[ 1 - \cos^2(t) = \sin^2(t) \]
Substitute \(\sin^2(t)\) into the expression:
\[ \frac{\sin^2(t)}{\cos^2(t)} \]
### Step 4: Simplify Further
Recognize that:
\[ \frac{\sin^2(t)}{\cos^2(t)} = \tan^2(t) \]
Since the given expression simplifies to \( \sin^2(t) \), the identity is verified:
\[ \boxed{\sin^2(t)} \]
By carefully substituting identities and simplifying step-by-step, we verify that:
\[ \frac{\sec(t) - \cos(t)}{\sec(t)}
Expert Solution
Step 1
Here question number is not mentioned, so we solve first question.
For more help, please upload the question and mention the question number.
Explanation:
Given that,
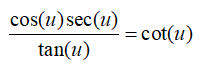
Step by step
Solved in 2 steps with 5 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning