Transform the following grammar to a grammar without left-recursive rules. S — A| В А — ААА | а | В B → BBb | b
Transform the following grammar to a grammar without left-recursive rules. S — A| В А — ААА | а | В B → BBb | b
Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:James Kurose, Keith Ross
Chapter1: Computer Networks And The Internet
Section: Chapter Questions
Problem R1RQ: What is the difference between a host and an end system? List several different types of end...
Related questions
Question

Transcribed Image Text:**Transform the Following Grammar to a Grammar Without Left-Recursive Rules**
Given Grammar:
1. \( S \to A \mid B \)
2. \( A \to AAA \mid a \mid B \)
3. \( B \to BBb \mid b \)
To convert the given grammar to a form without left recursion, the direct left recursion in the rules for \( A \) and \( B \) must be resolved by introducing new non-terminal symbols.
### Explanation of the Original Grammar
The original grammar consists of three production rules.
- The start symbol is \( S \), which can be replaced with either \( A \) or \( B \).
- The non-terminal \( A \) includes a left-recursive rule \( A \to AAA \), as well as options to replace with \( a \) or \( B \).
- The non-terminal \( B \) contains another left-recursive rule \( B \to BBb \), and can also resolve to \( b \).
### Steps to Remove Left Recursion
For each non-terminal with left recursion, introduce a new non-terminal:
1. **Convert \( A \):**
- Identify left-recursive and non-left-recursive parts:
- Left-recursive: \( AAA \)
- Non-left-recursive: \( a \), \( B \)
- Introduce \( A' \) to handle left recursion:
- Convert \( A \) to: \( A \to aA' \mid BA' \)
- Define \( A' \) with recursive production: \( A' \to AA' \mid \epsilon \)
2. **Convert \( B \):**
- Identify left-recursive and non-left-recursive parts:
- Left-recursive: \( BBb \)
- Non-left-recursive: \( b \)
- Introduce \( B' \) for left recursion:
- Convert \( B \) to: \( B \to bB' \)
- Define \( B' \) with recursion: \( B' \to BbB' \mid \epsilon \)
The resulting grammar will have no left recursion:
1. \( S \to A \mid B \)
2. \( A \to aA' \mid BA' \)
3. \( A' \to AA' \mid \epsilon \)
4. \( B \to bB' \)
5. \(
Expert Solution
Step 1
Assume that the set of all A-productions has the form
A  A A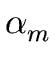 | | |
where no ![]() begins with an A and where
begins with an A and where ![]()
![]()
![]() holds for every i = 1 ... m. Then we replace these A-productions by
holds for every i = 1 ... m. Then we replace these A-productions by
|
Step by step
Solved in 2 steps with 22 images

Recommended textbooks for you

Computer Networking: A Top-Down Approach (7th Edi…
Computer Engineering
ISBN:
9780133594140
Author:
James Kurose, Keith Ross
Publisher:
PEARSON

Computer Organization and Design MIPS Edition, Fi…
Computer Engineering
ISBN:
9780124077263
Author:
David A. Patterson, John L. Hennessy
Publisher:
Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:
9781337569330
Author:
Jill West, Tamara Dean, Jean Andrews
Publisher:
Cengage Learning

Computer Networking: A Top-Down Approach (7th Edi…
Computer Engineering
ISBN:
9780133594140
Author:
James Kurose, Keith Ross
Publisher:
PEARSON

Computer Organization and Design MIPS Edition, Fi…
Computer Engineering
ISBN:
9780124077263
Author:
David A. Patterson, John L. Hennessy
Publisher:
Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:
9781337569330
Author:
Jill West, Tamara Dean, Jean Andrews
Publisher:
Cengage Learning

Concepts of Database Management
Computer Engineering
ISBN:
9781337093422
Author:
Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:
Cengage Learning

Prelude to Programming
Computer Engineering
ISBN:
9780133750423
Author:
VENIT, Stewart
Publisher:
Pearson Education

Sc Business Data Communications and Networking, T…
Computer Engineering
ISBN:
9781119368830
Author:
FITZGERALD
Publisher:
WILEY