Three electrons and one proton are at rest, all at an approximate infinite distance away from each other. This original arrangement of the four particles is defined as having zero electrical potential energy. 1.Now, with the electron remaining fixed at the origin, how much work is required to bring one of the remaining electrons from infinity to within a distance of 1.00 m from the first electron? The other two particles remain at infinity. If this second electron was subsequently released, how fast would it be traveling once it returned to infinity? In part (2) of the problem, if both electrons are released, what is the instantaneous acceleration of either electron after they have repelled each other and are currently 4.60 m apart? Would this acceleration remain constant as they continued to repel each other?
Three electrons and one proton are at rest, all at an approximate infinite distance away from each other. This original arrangement of the four particles is defined as having zero electrical potential energy.
1.Now, with the electron remaining fixed at the origin, how much work is required to bring one of the remaining electrons from infinity to within a distance of 1.00 m from the first electron? The other two particles remain at infinity. If this second electron was subsequently released, how fast would it be traveling once it returned to infinity? In part (2) of the problem, if both electrons are released, what is the instantaneous acceleration of either electron after they have repelled each other and are currently 4.60 m apart? Would this acceleration remain constant as they continued to repel each other?
Work (W) done to bring a charge (q1) from infinity to a distance (r) from another charge (q2) may be given by Coulomb’s formula as follows:
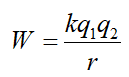
Here, k is Coulomb’s constant.
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images
