This rectangular loop is rotating at 6000 rpm in a uniform magnetic flux density of B = y 50 mT. Determine the current induced in the loop if its internal resistance is 0.5 92.
This rectangular loop is rotating at 6000 rpm in a uniform magnetic flux density of B = y 50 mT. Determine the current induced in the loop if its internal resistance is 0.5 92.
Related questions
Question
Homework Help

Transcribed Image Text:### Problem Description
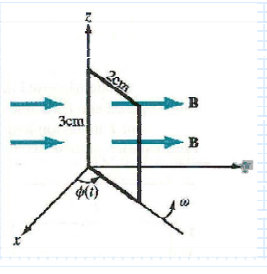
This rectangular loop is rotating at 6000 rpm in a uniform magnetic flux density of \( B = y \, 50 \, \text{mT} \). Determine the current induced in the loop if its internal resistance is \( 0.5 \, \Omega \).
### Diagram Explanation
- **Axes**: The diagram is drawn in a 3D coordinate system with labeled axes \( x \), \( y \), and \( z \).
- **Loop**: There is a rectangular loop oriented in the \( yz \)-plane with its center at the origin.
- **Dimensions**: The sides of the rectangle are both \( 3 \, \text{cm} \).
- **Magnetic Field**: There is a uniform magnetic field, denoted by \( \mathbf{B} \), shown as arrows pointing in the positive \( y \)-direction.
- **Rotation**: The loop is rotating about the \( x \)-axis with angular velocity \( \omega \).
- **Angle**: The angle \( \phi(t) \) illustrates the angular position of the loop as it rotates.
### Solution Steps
1. **Induced EMF Calculation**: Use Faraday’s Law of Electromagnetic Induction to calculate the induced electromotive force (EMF) in the loop.
2. **Current Calculation**: Use Ohm’s Law to determine the current induced in the loop by dividing the induced EMF by the internal resistance \( 0.5 \, \Omega \).
### Key Concepts
- **Faraday’s Law**: The induced EMF in a loop is proportional to the rate of change of magnetic flux through the loop.
- **Ohm’s Law**: Current through a resistor is equal to the voltage across it divided by its resistance.
This setup is a classic problem in electromagnetism, demonstrating the principles of electromagnetic induction in a rotating loop within a magnetic field.
Expert Solution
Step 1: Determine the given data:
Step by step
Solved in 3 steps with 4 images
