Therefore we obtain that U1 +h +P U2 12 <2+P U2 12 - l2 - P U2 U1 + P + U2 + p- U1 U1 U2 - 1 12 - P < 0, U1 + P + U2 + p U1 + (U2 – 12) + U2 <0. (U1 – 1) In this here if p e (0, 5) then 1- p > 0, U1 > 0. 1- p 12 U2 Thus, we get that -h = 0, U2 – 12 = 0. So, U1 = l1 and U2 = l2. The proof is completed as desired.
Therefore we obtain that U1 +h +P U2 12 <2+P U2 12 - l2 - P U2 U1 + P + U2 + p- U1 U1 U2 - 1 12 - P < 0, U1 + P + U2 + p U1 + (U2 – 12) + U2 <0. (U1 – 1) In this here if p e (0, 5) then 1- p > 0, U1 > 0. 1- p 12 U2 Thus, we get that -h = 0, U2 – 12 = 0. So, U1 = l1 and U2 = l2. The proof is completed as desired.
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
Show me the steps of deremine red and inf is here i need evey I need all the details step by step and inf is here

Transcribed Image Text:Motivated by difference equations and their systems, we consider the following
system of difference equations
Уп
Xn
Xn+1 = A +B
, Yn+1 = A + B
(1)
2.
n-1
n-1
where A and B are positive numbers and the initial values are positive numbers. In
From this, system (1) transform into following system:
tn
In+1 = 1+P
Zn
Zn+1 =
(2)
%3D
n-1
n-1
where p = > 0. From now on, we study the system (2).

Transcribed Image Text:Theorem 7 Assume that 0 < p < . Then the positive equilibrium point of system (2)
is globally asymptotically stable.
Proof We have from Theorem 5,
1 < l1 = lim inftn < M1,
n-00
1 < l2 = lim infzn < M2,
n-00
1 < U1 = lim supt, < M1,
%3D
n-00
1 < U2 = lim supzn < M2.
n00
By system (2), we can write
12
U2
U1 <1+ p,h 2 1+ p-
U1
U2 1+P221+ p;
Hence we have
U2
< Ujl2 <2+ p
12
12
U1
U2 + p-
< Uzlı <li+ PT
U2
Therefore we obtain that
U2
<12+ p
U1
+l1 + p-
12
Ui + PU,
+ U2 + p
U2
12
U2
р
12
U1
12
12
U2
Ui + PU1
р
<0,
+ U2 + P
<0.
(U1 – 1)
+ (U2 – 12)
12
U2
U1
In this here if p e (0, 5) then
1- p
> 0,
U1
1- P
> 0.
U2
Thus, we get that
U1-1 = 0, U2 - 12 = 0.
So, U1 = l1 and U2 = 12. The proof is completed as desired.
%3D
Expert Solution
Step 1
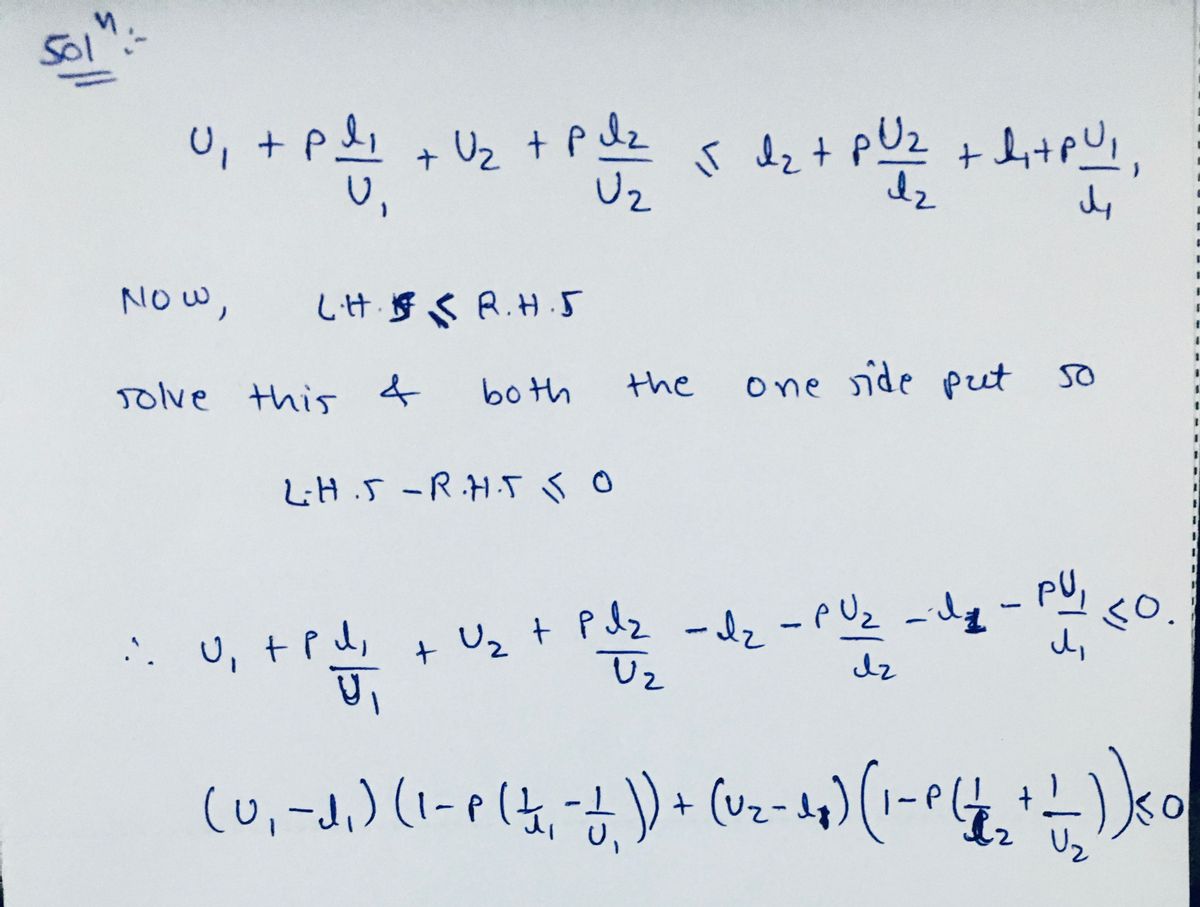
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning