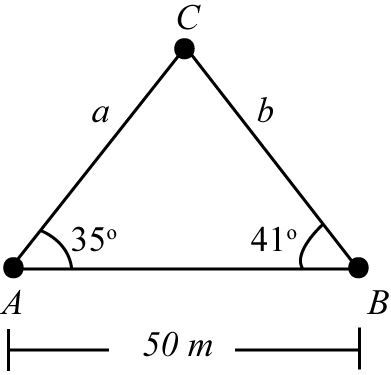
There are two lifeguard stations along the shoreline. Station B is 50 meters east of station A. A troubled swimmer is spotted by lifeguards at both stations. If the troubled swimmer is spotted at a 35° angle from the guard at station A and a 41° angle from station B (swimmer between A and B), which lifeguard is the shortest distance from the swimmer? By how many meters?
Ratios
A ratio is a comparison between two numbers of the same kind. It represents how many times one number contains another. It also represents how small or large one number is compared to the other.
Trigonometric Ratios
Trigonometric ratios give values of trigonometric functions. It always deals with triangles that have one angle measuring 90 degrees. These triangles are right-angled. We take the ratio of sides of these triangles.
There are two lifeguard stations along the shoreline. Station B is 50 meters east of station A. A troubled swimmer is spotted by lifeguards at both stations. If the troubled swimmer is spotted at a 35° angle from the guard at station A and a 41° angle from station B (swimmer between A and B),
which lifeguard is the shortest distance from the swimmer? By how many meters?
Given data:
The distance between both stations is AB =50 m.
The angle made by a swimmer with station A is ∠A=35°.
The angle made by a swimmer with station B is ∠B=41°.
The below figure represents the position of the swimmer C.
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images









