The water flows from the nozzle through a 180-degree elbow. For example, the pipe diameter D-75mm, the nozzle diameter d=25mm, and the pressure gauge at the front of the pipe reads 60kPa. Find the force of the upper, middle and lower bolts at the flange joint 1-1 position. Assuming that four bolts are installed at the up, down, front and back, the cross-center distance of the four bolts is 150mm, the weight of the elbow and the water is 100N, and the acting position is shown in the figure.
The water flows from the nozzle through a 180-degree elbow. For example, the pipe diameter D-75mm, the nozzle diameter d=25mm, and the pressure gauge at the front of the pipe reads 60kPa. Find the force of the upper, middle and lower bolts at the flange joint 1-1 position. Assuming that four bolts are installed at the up, down, front and back, the cross-center distance of the four bolts is 150mm, the weight of the elbow and the water is 100N, and the acting position is shown in the figure.
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 1 images
Hello. So the total force on the bolts are equal to the resultant of fv and fh as shown in the picture? Please see my solution if it is correct.
So Fh in your drawing is equal to the fh on the bolt? I am confused. The question says find the force on the bolt. Is fh referring to the horizontal force on the bolt? Thank you
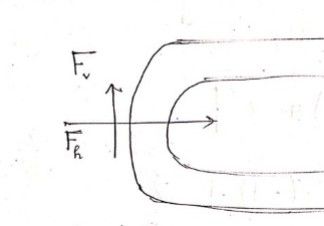
by Bartleby ExpertIs the Fh equal to the force made on the bolts at flange 1-1 in this question? And can you please plug in the values and the answer so than I can compare with my solution? Please
The water flows from the nozzle through a 180-degree elbow. For example, the pipe diameter D-75mm, the nozzle diameter d=25mm, and the pressure gauge at the front of the pipe reads 60kPa. Find the force of the upper, middle and lower bolts at the flange joint 1-1 position. Assuming that four bolts are installed at the up, down, front and back, the cross-center distance of the four bolts is 150mm, the weight of the elbow and the water is 100N, and the acting position is shown in the figure.
by Bartleby ExpertOne last question.
Why can't we use the summation of forces is equal to momentum change or the momentum equation in this problem?
So it becomes like in the image.
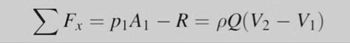
by Bartleby ExpertThe horizontal force due to water acting on the bolt (Fh):
Fh=ρ×A1×V1×V1--V2 Fh=1000×π4×0.0752×1.254×1.254+11.286(
Fh)=69.472
This is the only part I did not understand how to get. Can you please explain more?
I arrived with this equation,
-P1A1 - P2A2 (cancelled since atmos. Pres.) +Fh = rho A1v1 (v2-v1)
Why did P1A1 disappear in your solution?
How did you come up with (v1 - - v2) ?
What is the control volume?
Why did you not do a summation of forces is equal to change in momentum but instead go immediately to getting the horizontal force acting on the bolt?
by Bartleby Expert
