Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
ChapterP: Preliminary Concepts
SectionP.CT: Test
Problem 1CT
Related questions
Concept explainers
Ratios
A ratio is a comparison between two numbers of the same kind. It represents how many times one number contains another. It also represents how small or large one number is compared to the other.
Trigonometric Ratios
Trigonometric ratios give values of trigonometric functions. It always deals with triangles that have one angle measuring 90 degrees. These triangles are right-angled. We take the ratio of sides of these triangles.
Question
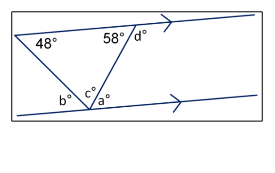
![**Problem 5: Find the value of all the variables.**
The image shows a quadrilateral with various labeled angles:
1. Inside the quadrilateral, there is a triangle with angles 48° and 58°.
2. The quadrilateral extends with a transversal line, forming exterior angles labeled as \(a^\circ\), \(b^\circ\), \(c^\circ\), and \(d^\circ\).
**Explanation:**
- The angle labeled 48° and one labeled \(b^\circ\) are on the same straight line, suggesting they are supplementary. Therefore, \(b = 132^\circ\).
- Similarly, the angle labeled 58° and the angle labeled \(d^\circ\) are on the same straight line, also suggesting they are supplementary. Therefore, \(d = 122^\circ\).
- The interior triangle angles (48°, 58°, and \(a^\circ\)) sum to 180°:
\[
a = 180^\circ - 48^\circ - 58^\circ = 74^\circ
\]
- Since angle \(c^\circ\) is an exterior angle to angle \(a^\circ\), we have \(c = a = 74^\circ\).
In summary:
- \(a = 74^\circ\)
- \(b = 132^\circ\)
- \(c = 74^\circ\)
- \(d = 122^\circ\)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F70dd3339-9069-4b36-b997-58da94976e85%2F749f71ed-4dd5-447b-8539-710b24765d35%2Frioix2o_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem 5: Find the value of all the variables.**
The image shows a quadrilateral with various labeled angles:
1. Inside the quadrilateral, there is a triangle with angles 48° and 58°.
2. The quadrilateral extends with a transversal line, forming exterior angles labeled as \(a^\circ\), \(b^\circ\), \(c^\circ\), and \(d^\circ\).
**Explanation:**
- The angle labeled 48° and one labeled \(b^\circ\) are on the same straight line, suggesting they are supplementary. Therefore, \(b = 132^\circ\).
- Similarly, the angle labeled 58° and the angle labeled \(d^\circ\) are on the same straight line, also suggesting they are supplementary. Therefore, \(d = 122^\circ\).
- The interior triangle angles (48°, 58°, and \(a^\circ\)) sum to 180°:
\[
a = 180^\circ - 48^\circ - 58^\circ = 74^\circ
\]
- Since angle \(c^\circ\) is an exterior angle to angle \(a^\circ\), we have \(c = a = 74^\circ\).
In summary:
- \(a = 74^\circ\)
- \(b = 132^\circ\)
- \(c = 74^\circ\)
- \(d = 122^\circ\)
Expert Solution
Step 1
we have been given
we have to determine the all the unknown angles.
Given the two given lines are parallel.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning