The total revenue curve of a firm is R(q) = 40q − 12q and its 1 400 average cost A(q) = q − 12.85q + 20 + , where q is the firm s output. 30 q i. Derive an expression C(q) for the firm s total cost function. ii. Derive an expression Π(q) for the firm s profit function. iii. Is the rate of change of profit increasing or decreasing when the ouput level of the firm is 10 units? iv. Determine the level of output for which the firm s profit is maximized. v. What is the firms s maximum profit?
(b) The total revenue curve of a firm is R(q) = 40q − 12q and its
1 400
average cost A(q) = q − 12.85q + 20 + , where q is the firm s output.
30 q
i. Derive an expression C(q) for the firm s total cost function. ii. Derive an expression Π(q) for the firm s profit function.
iii. Is the rate of change of profit increasing or decreasing when the
ouput level of the firm is 10 units?
iv. Determine the level of output for which the firm s profit is maximized.
v. What is the firms s maximum profit?
According to the given information, the total revenue and average cost function is given as:
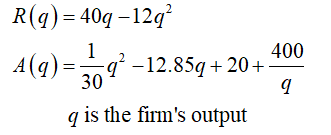
For part (i) it is required to derive the expression C(q) for the firm’s total cost function.

For part (ii) it is required to derive the expression π(q) for the firms profit function.
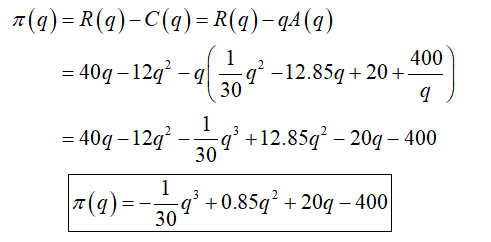
For part (iii) it is required to tell whether the rate of change of profit increasing or decreasing when output level is 10 units.
A function f(x) is increasing if f’(x) > 0 and f’(x) is decreasing if f’(x) < 0.
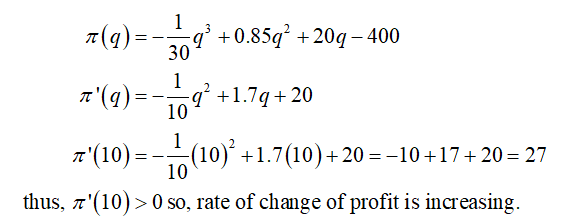
Step by step
Solved in 7 steps with 7 images









