The system of linear equations is in upper-triangular form. Find all solutions of the system. (Use the parameters x, y, and z as necessary. If the system is inconsistent, enter INCONSISTENT.) + y + z = -9 3y2z=-11 8z = -16 (x, y, z) = -3, -3, 2 )
The system of linear equations is in upper-triangular form. Find all solutions of the system. (Use the parameters x, y, and z as necessary. If the system is inconsistent, enter INCONSISTENT.) + y + z = -9 3y2z=-11 8z = -16 (x, y, z) = -3, -3, 2 )
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
![**Title:** Solving a System of Linear Equations in Upper-Triangular Form
The system of linear equations is in upper-triangular form. Find all solutions of the system. (Use the parameters \(x\), \(y\), and \(z\) as necessary. If the system is inconsistent, enter INCONSISTENT.)
\[
\begin{cases}
2x + y + z = -9 \\
3y - 2z = -11 \\
8z = -16
\end{cases}
\]
The solution for the system is:
\[
(x, y, z) = \boxed{(-3, -3, -2)}
\]
**Explanation:**
This problem involves solving a system of linear equations that has been presented in an upper-triangular form. The equations are structured in a way that the variables form a triangular pattern, simplifying the use of back substitution to find all variables' values.
- **Equation 1:** \(2x + y + z = -9\)
- **Equation 2:** \(3y - 2z = -11\)
- **Equation 3:** \(8z = -16\)
The final solution points that \((x, y, z)\) are \((-3, -3, -2)\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9f36f111-f1bc-4b8c-9508-d8f50a3e95e1%2F272fddac-9ca8-4c90-a626-08d16f776de8%2Fze5qvq_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Title:** Solving a System of Linear Equations in Upper-Triangular Form
The system of linear equations is in upper-triangular form. Find all solutions of the system. (Use the parameters \(x\), \(y\), and \(z\) as necessary. If the system is inconsistent, enter INCONSISTENT.)
\[
\begin{cases}
2x + y + z = -9 \\
3y - 2z = -11 \\
8z = -16
\end{cases}
\]
The solution for the system is:
\[
(x, y, z) = \boxed{(-3, -3, -2)}
\]
**Explanation:**
This problem involves solving a system of linear equations that has been presented in an upper-triangular form. The equations are structured in a way that the variables form a triangular pattern, simplifying the use of back substitution to find all variables' values.
- **Equation 1:** \(2x + y + z = -9\)
- **Equation 2:** \(3y - 2z = -11\)
- **Equation 3:** \(8z = -16\)
The final solution points that \((x, y, z)\) are \((-3, -3, -2)\).
Expert Solution
Step 1
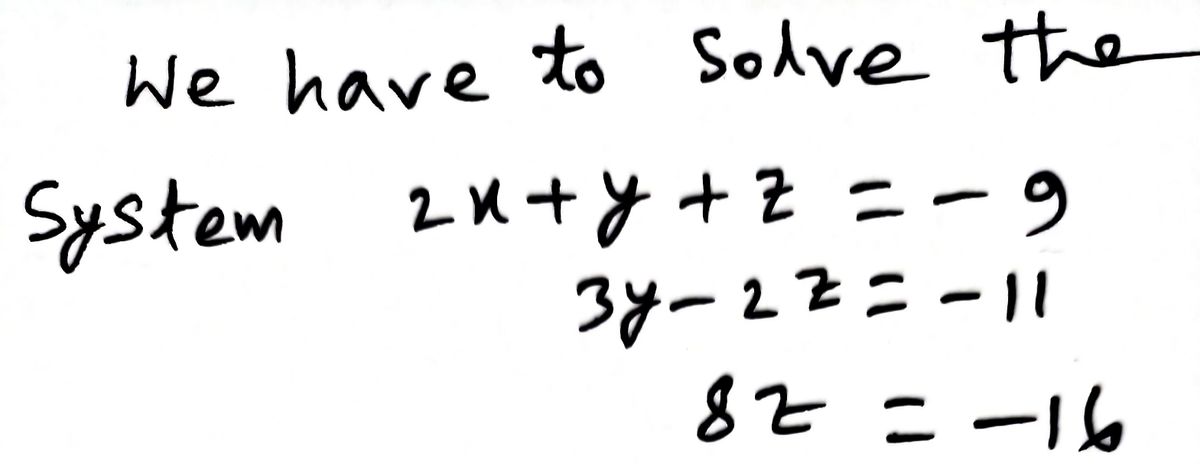
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education