The remaining problems require you to construct a mathematical proof by induction. Remember, if you don't make use of the inductive hypothesis, there is no way to finish the proof correctly! 9. The following formula is called De'Moivre's Formula: (cos+ i sin 0)" = cos(ne)+ i sin(ne) Prove De'Moivre's formula for all integers n ≥0. (Hint: you will need a trig identity from Precalculus).
The remaining problems require you to construct a mathematical proof by induction. Remember, if you don't make use of the inductive hypothesis, there is no way to finish the proof correctly! 9. The following formula is called De'Moivre's Formula: (cos+ i sin 0)" = cos(ne)+ i sin(ne) Prove De'Moivre's formula for all integers n ≥0. (Hint: you will need a trig identity from Precalculus).
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![### Inductive Proof Exercise: DeMoivre's Formula
**Instructions for Inductive Proof:**
The remaining problems require you to construct a mathematical proof by induction. Remember, if you don’t make use of the inductive hypothesis, there is no way to finish the proof correctly!
#### Problem 9
The following formula is called DeMoivre’s Formula:
\[
\left( \cos \theta + i \sin \theta \right)^n = \cos(n\theta) + i \sin(n\theta)
\]
**Task**: Prove DeMoivre’s formula for all integers \( n \geq 0 \).
**Hint**: You will need a trig identity from Precalculus.
---
**Explanation:**
In this problem, you are asked to establish the truth of DeMoivre’s formula using mathematical induction. The formula relates powers of complex numbers in polar form to their corresponding trigonometric identities, a fundamental result in complex number theory.
**Steps for Induction**:
1. **Base Case**: Verify the formula for \( n = 0 \).
2. **Inductive Step**: Assume the formula holds for some arbitrary \( n = k \). Show it holds for \( n = k + 1 \) using your assumption.
Mathematical proofs by induction often require recalling foundational trigonometric identities, so it’s beneficial to review those, especially double angle formulas and other relationships that tie into Euler’s formula.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9c836437-a2a4-49ad-8637-6abf33735fd4%2F9beefaae-0cc4-42fe-a6f0-da25b9dfb4c0%2Feq3cgik_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Inductive Proof Exercise: DeMoivre's Formula
**Instructions for Inductive Proof:**
The remaining problems require you to construct a mathematical proof by induction. Remember, if you don’t make use of the inductive hypothesis, there is no way to finish the proof correctly!
#### Problem 9
The following formula is called DeMoivre’s Formula:
\[
\left( \cos \theta + i \sin \theta \right)^n = \cos(n\theta) + i \sin(n\theta)
\]
**Task**: Prove DeMoivre’s formula for all integers \( n \geq 0 \).
**Hint**: You will need a trig identity from Precalculus.
---
**Explanation:**
In this problem, you are asked to establish the truth of DeMoivre’s formula using mathematical induction. The formula relates powers of complex numbers in polar form to their corresponding trigonometric identities, a fundamental result in complex number theory.
**Steps for Induction**:
1. **Base Case**: Verify the formula for \( n = 0 \).
2. **Inductive Step**: Assume the formula holds for some arbitrary \( n = k \). Show it holds for \( n = k + 1 \) using your assumption.
Mathematical proofs by induction often require recalling foundational trigonometric identities, so it’s beneficial to review those, especially double angle formulas and other relationships that tie into Euler’s formula.
Expert Solution
Step 1
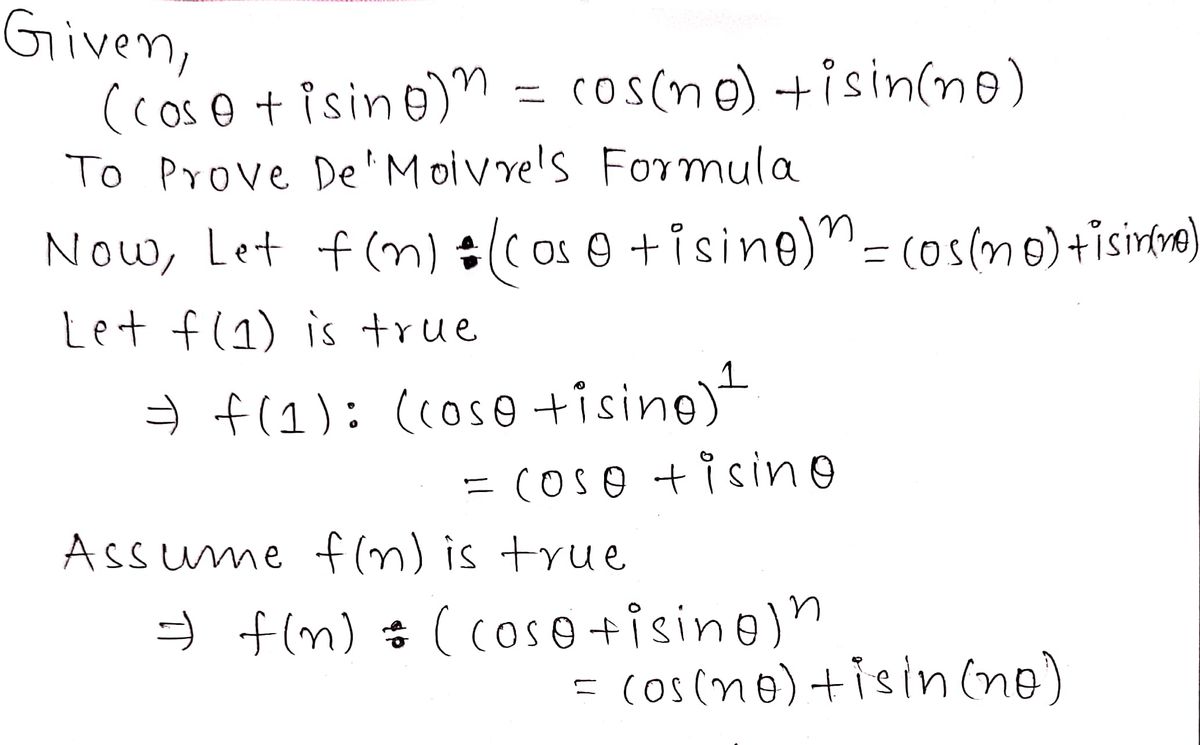
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

