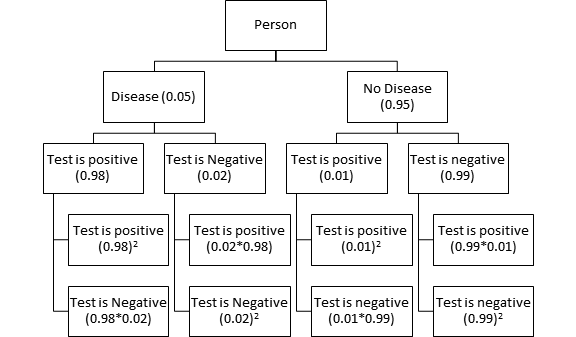
The probability that an individual randomly selected from a particular population has a certain disease is 0.05. A diagnostic test correctly detects the presence of the disease 98% of the time and correctly detects the absence of the disease 99% of the time. If the test is applied twice, the two test results are independent, and both are positive, what is the (posterior) probability that the selected individual has the disease? [Hint: Tree diagram with first-generation branches corresponding to Disease and No Disease, and second- and third-generation branches corresponding to results of the two tests.]
Compound Probability
Compound probability can be defined as the probability of the two events which are independent. It can be defined as the multiplication of the probability of two events that are not dependent.
Tree diagram
Probability theory is a branch of mathematics that deals with the subject of probability. Although there are many different concepts of probability, probability theory expresses the definition mathematically through a series of axioms. Usually, these axioms express probability in terms of a probability space, which assigns a measure with values ranging from 0 to 1 to a set of outcomes known as the sample space. An event is a subset of these outcomes that is described.
Conditional Probability
By definition, the term probability is expressed as a part of mathematics where the chance of an event that may either occur or not is evaluated and expressed in numerical terms. The range of the value within which probability can be expressed is between 0 and 1. The higher the chance of an event occurring, the closer is its value to be 1. If the probability of an event is 1, it means that the event will happen under all considered circumstances. Similarly, if the probability is exactly 0, then no matter the situation, the event will never occur.
The
Let X be a random variable such that
X: Person has the disease
P: the test is positive
N: the test is negative
The following information is provided in the question
Now,
Similarly
Now, conducting the test again,
Since the test results are independent,
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images









