The probability of a machine producing a defective part, in one day, is of 0.1. Think in two possible situations: the probability that the 18th piece produced on the day is the 4th defective and the probability that the 10th part produced on the day will be the 1st defective.
Addition Rule of Probability
It simply refers to the likelihood of an event taking place whenever the occurrence of an event is uncertain. The probability of a single event can be calculated by dividing the number of successful trials of that event by the total number of trials.
Expected Value
When a large number of trials are performed for any random variable ‘X’, the predicted result is most likely the mean of all the outcomes for the random variable and it is known as expected value also known as expectation. The expected value, also known as the expectation, is denoted by: E(X).
Probability Distributions
Understanding probability is necessary to know the probability distributions. In statistics, probability is how the uncertainty of an event is measured. This event can be anything. The most common examples include tossing a coin, rolling a die, or choosing a card. Each of these events has multiple possibilities. Every such possibility is measured with the help of probability. To be more precise, the probability is used for calculating the occurrence of events that may or may not happen. Probability does not give sure results. Unless the probability of any event is 1, the different outcomes may or may not happen in real life, regardless of how less or how more their probability is.
Basic Probability
The simple definition of probability it is a chance of the occurrence of an event. It is defined in numerical form and the probability value is between 0 to 1. The probability value 0 indicates that there is no chance of that event occurring and the probability value 1 indicates that the event will occur. Sum of the probability value must be 1. The probability value is never a negative number. If it happens, then recheck the calculation.
The
Negative Binomial Distribution: If we have a sequence of trials each having two outcomes, say Success and Failure, trials being independent and the probability of success, say p, remaining constant, the sequence is continued until a predefined number of successes, say r, have occurred. Then the distribution of the number of failures follows the negative binomial.
Let us assume X be a random variable denoting the number of trials needed for r successes.
Then , r and p being the parameters of the negative binomial distribution.
The probability mass function of X is given by,
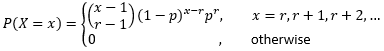
Step by step
Solved in 3 steps with 5 images









