The mean inspection time, using the current method of quality control, has been found over a long period of time to be 160 seconds. Your manager decides to introduce a new method of quality control aimed at reducing this to as short as possible and so she expects the new method to produce a smaller mean. A random sample of measurement of inspection time taken after the new method had become established gave the following distribution: Time (sec) 120 129 135 144 157 173 179 191 Number 1 3 2 3 4 3 3 4 Your manager thinks that the introduction of the new method of inspection has been very effective in reducing the inspection time. Using the data provided and assuming the inspection time to be normally distributed with a standard deviation of 28 seconds, test this hypothesis at 5% level of significance
The mean inspection time, using the current method of quality control, has been found over a long period of time to be 160 seconds. Your manager decides to introduce a new method of quality control aimed at reducing this to as short as possible and so she expects the new method to produce a smaller mean. A random sample of measurement of inspection time taken after the new method had become established gave the following distribution: Time (sec) 120 129 135 144 157 173 179 191 Number 1 3 2 3 4 3 3 4 Your manager thinks that the introduction of the new method of inspection has been very effective in reducing the inspection time. Using the data provided and assuming the inspection time to be normally distributed with a standard deviation of 28 seconds, test this hypothesis at 5% level of significance
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
The mean inspection time, using the current method of quality control, has been found over a long period of time to be 160 seconds. Your manager decides to introduce a new method of quality control aimed at reducing this to as short as possible and so she expects the new method to produce a smaller mean. A random sample of measurement of inspection time taken after the new method had become established gave the following distribution:
|
Time (sec) |
120 |
129 |
135 |
144 |
157 |
173 |
179 |
191 |
|
Number |
1 |
3 |
2 |
3 |
4 |
3 |
3 |
4 |
Your manager thinks that the introduction of the new method of inspection has been very effective in reducing the inspection time. Using the data provided and assuming the inspection time to be
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Can you explain how the highlighted boxes in the attached image a little better?
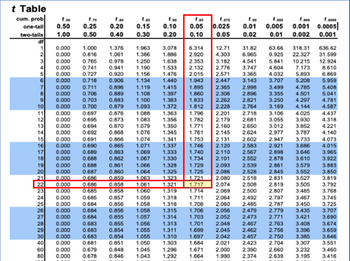
The T table i have, which is also attached( given the degree of freedom is 22) gives a value of 1.717?
Whereas you have given values of -1.64. Then a P value of 0.432? Can you explain further how you have reached these different figures?
![2
x - l
S/√n
=
At 5% level of significance. α = 0.05
Critical value
LLAR
=
=
& P-value
159 - 160
28
P
-0.1713
20.05 =-1.64
2 <0·1213]
0.432
$ Obtained from 2-table
lor Normal probability
calculator 4
Since. 2 > 2x
and P-value > α, hence
We accept to at 5% level of significance.
|1t μ = 160.
Conclude that, new method of inspection is not](https://content.bartleby.com/qna-images/question/c32c1e5f-b2a4-418c-8d03-158c2a8cd1bc/4a755818-e47d-483a-bc0c-096149b5d211/r77obol_processed.png)
Transcribed Image Text:2
x - l
S/√n
=
At 5% level of significance. α = 0.05
Critical value
LLAR
=
=
& P-value
159 - 160
28
P
-0.1713
20.05 =-1.64
2 <0·1213]
0.432
$ Obtained from 2-table
lor Normal probability
calculator 4
Since. 2 > 2x
and P-value > α, hence
We accept to at 5% level of significance.
|1t μ = 160.
Conclude that, new method of inspection is not
Transcribed Image Text:t Table
cum. prob
one-tail
two-tails 1.00
df
1
2
3
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
1.50
0.50
27
28
0.000 1.000
0.000
0.816
1.00
1.75
0.25
0.20
0.50 0.40
0.000 0.697
0.000
0.695
0.000 0.694
0.000 0.692
1.376
1.061 1.386
0.000
0.765
0.978
1.250
0.741 0.941 1.190
0.000
0.000
0.727
0.000 0.718
0.000
0.711
0.000 0.706
0.000
0.703
0.000
0.700
0.000
0.000
0.000
0.000
0.920
0.906
1.90
0.10
0.15
0.30 0.20
1.156
1.134 1.440
0.896
1.119 1.415
0.889
1.108
1.397
0.883
1.100
1.383
0.879 1.093 1.372
1.363
1.356
0.876
0.873
0.870
0.868
1.963 3.078
1.886
1.638
2.353
1.533 2.132
1.476 2.015
1.088
1.083
1.079
1.076
1.350
1.345
0.691
0.866
1.074
0.690 0.865 1.071
0.689
0.863 1.069
0.688 0.862 1.067 1.330
0.688 0.861 1.066 1.328
0.860 1.064
0.000
0.000
0.687
1.325
0.000
0.686
0.859
1.063
1.323
0.000
0.686 0.858
1.061
1.321
0.000 0.685
0.858 1.060
1.319
0.000 0.685 0.857 1.059 1.318
0.000 0.684 0.856 1.058 1.316
0.000 0.684 0.856 1.058 1.315
0.000 0.684 0.855 1.057 1.314
1.056
1.313
0.000 0.683 0.855
0.000 0.683 0.854
29
1.055
1.311
30
1.697
0.000
0.000 0.681
1.055 1.310
1.050 1.303 1.684
40
0.683 0.854
0.851
0.848
80 0.000 0.678 0.846
60
0.000 0.679
1.296 1.671
1.045
1.043
1.292 1.664
199
1305
tas
1.375
0.05 0.025 0.01 0.005 0.001
0.10 0.05 0.02
6.314
12.71
2.920 4.303
1.341
1.337
1.333
31.82
6.965
4.541
3.747
3.365
2.571
1.943 2.447 3.143 3.707
1.895 2.365 2.998
1.860 2.306 2.896
1.833 2.262 2.821
1.812
3.182
2.776
1.796
2.201
1.782 2.179
1.771
1.729
1.725
1.721
5.208
3.499 4.785
3.355 4.501
3.250 4.297
2.228 2.764 3.169 4.144
3.106 4.025
2.718
2.681 3.055 3.930
2.160 2.650 3.012 3.852
1.761 2.145 2.624 2.977 3.787
1.753 2.131 2.602 2.947 3.733
2.583 2.921 3.686
1.746 2.120
1.740 2.110
3.646
1.734
2.567 2.898
2.878
2.539 2.861 3.579
3.610
2.528
2.845
3.552
2.518
2.831 3.527
2.508
2.819
2.500
2.807
2.101 2.552
t905
0.0005
0.01 0.002 0.001
2.093
2.086
2.080
2.074
2.069
1.717
1.714
1.711
2.064
1.708 2.060
1.706 2.056
1.703
1.701
1.699
63.66 318.31 636.62
9.925 22.327
31.599
5.841 10.215 12.924
4.604
7.173
4.032
5.893
3992
2.492
2.797
2.485 2.787
2.479 2.779
2.052 2.473 2.771
2.048 2.467
2.045 2.462 2.756
2.042
2.021
2.000
1.990
3.505
3.485
8.610
6.869
5.959
3.421
2.763 3.408
3.396
2.457 2.750 3.385
2.423 2.704
3.307
2.390
2.660
3.232
2.374 2.639 3.195
5.408
5.041
4.781
4.587
4.437
4.318
4.221
4.140
4.073
4.015
3.965
3.922
3.792
3.768
3.467 3.745
3.450
3.725
3.435
3.883
3.850
3.819
3.707
3.690
3.674
3.659
3.646
3.551
3.460
3.416
Solution
by Bartleby ExpertRecommended textbooks for you
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON
The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman