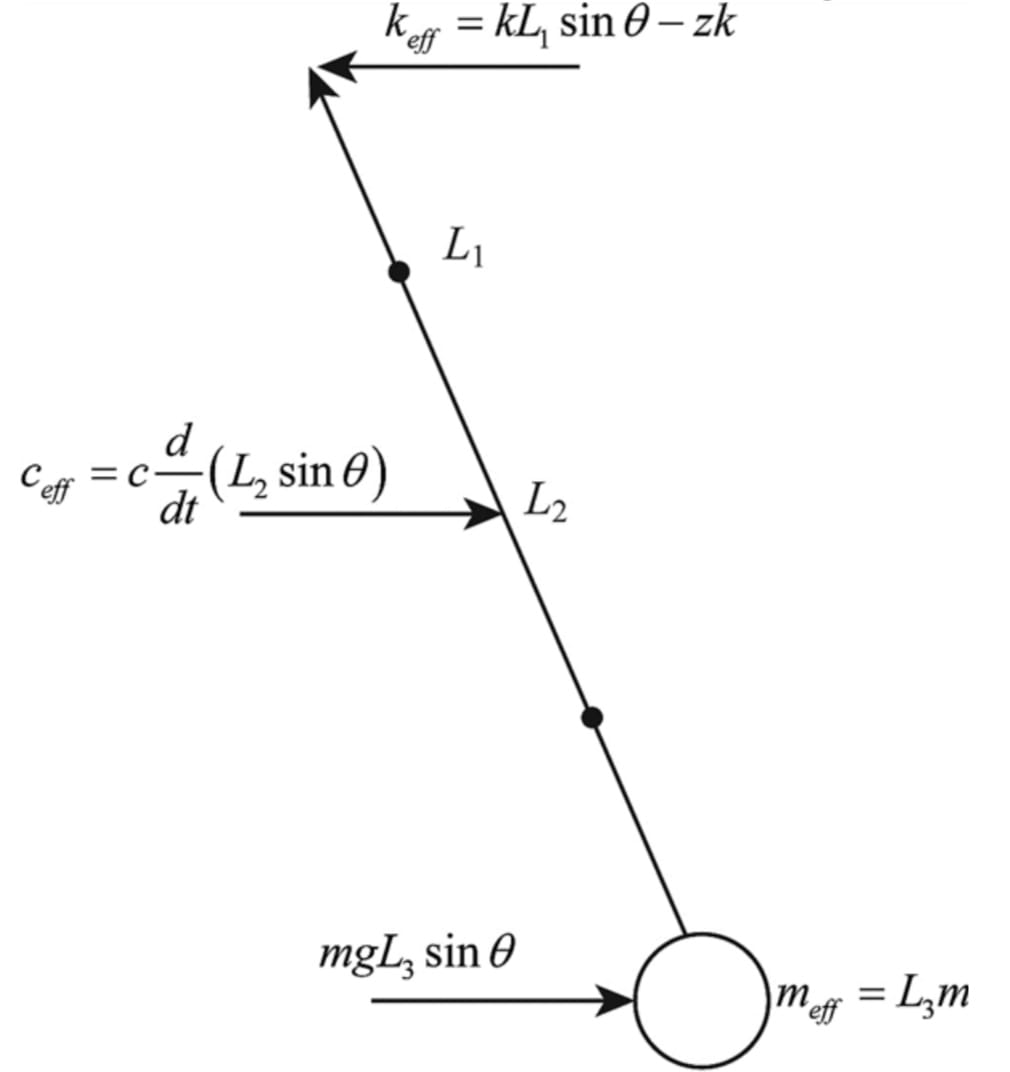
The mass m in the given figure is attached to a rigid rod with an inertia /about the pivot and negligible pivot friction. The input is the displacement z. When z= 0 = 0, the spring is at its free length. m a. Assuming that 0 is small, identify the equation of motion for 0 with z as the input. b. Use the Laplace transform method to determine the characteristic equation for this system. c. Solve this for the step response, 0(t), for the following system parameters and if the amplitude of the input step is z = 4 mm: System_Parameters - (k = 100000.0 c= 1200.0 L, = 0.03 L2=0.04 L3=0.1 m=2.0 I=0.8 g=9.81 units : k~ N; c ~N.s; L, L2, L2 ~ m; M ~ kg; I ~ kg · m²; g ~ -; m m m
The mass m in the given figure is attached to a rigid rod with an inertia /about the pivot and negligible pivot friction. The input is the displacement z. When z= 0 = 0, the spring is at its free length. m a. Assuming that 0 is small, identify the equation of motion for 0 with z as the input. b. Use the Laplace transform method to determine the characteristic equation for this system. c. Solve this for the step response, 0(t), for the following system parameters and if the amplitude of the input step is z = 4 mm: System_Parameters - (k = 100000.0 c= 1200.0 L, = 0.03 L2=0.04 L3=0.1 m=2.0 I=0.8 g=9.81 units : k~ N; c ~N.s; L, L2, L2 ~ m; M ~ kg; I ~ kg · m²; g ~ -; m m m
Related questions
Question
Please show how to solve part a, b, and c, cleary. State why you chose the formulas and what each variable represents. Thank you!!

Transcribed Image Text:The mass m in the given figure is attached to a rigid rod with an inertia / about the pivot and negligible pivot friction. The input is the displacement z. When z= 0 = 0,
the spring is at its free length.
a. Assuming that 0 is small, identify the equation of motion for 0 with z as the input.
b. Use the Laplace transform method to determine the characteristic equation for this system.
c. Solve this for the step response, 0(t), for the following system parameters and if the amplitude of the input step is z = 4 mm:
System_Parameters =
(k = 100000.0 c= 1200.0 L, = 0.03 L2=0.04 L3= 0.1 m=2.0 I=0.8 g=9.81
units : k - ; c ~N.s; L1, L2, L2 ~ m; M ~ kg; I ~ kg · m²; g ~ ;
N
m
т
Expert Solution
Step 1
Consider the spring is at its free length when and .
The modified functional diagram of pendulum with a concentrated mass as shown in the figure below.
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images
