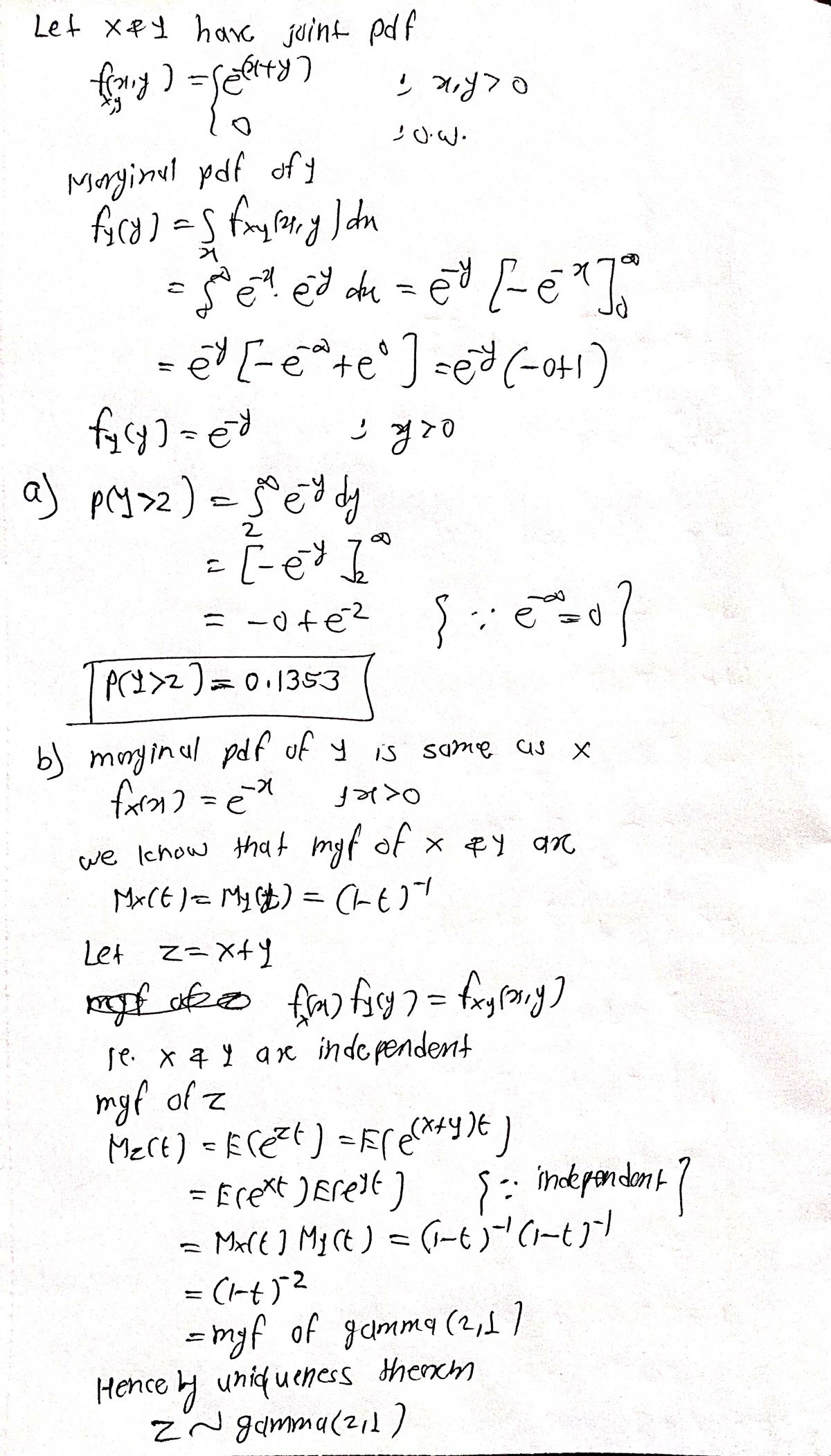1 Combinatorial Analysis 2 Axioms Of Probability 3 Conditional Probability And Independence 4 Random Variables 5 Continuous Random Variables 6 Jointly Distributed Random Variables 7 Properties Of Expectation 8 Limit Theorems 9 Additional Topics In Probability 10 Simulation Chapter1: Combinatorial Analysis
Chapter Questions Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and... Problem 1.2P: How many outcome sequences are possible ten a die is rolled four times, where we say, for instance,... Problem 1.3P: Twenty workers are to be assigned to 20 different jobs, one to each job. How many different... Problem 1.4P: John, Jim, Jay, and Jack have formed a band consisting of 4 instruments if each of the boys can play... Problem 1.5P: For years, telephone area codes in the United States and Canada consisted of a sequence of three... Problem 1.6P: A well-known nursery rhyme starts as follows: As I was going to St. Ives I met a man with 7 wives.... Problem 1.7P: a. In how many ways can 3 boys and 3 girls sit in a row? b. In how many ways can 3 boys and 3 girls... Problem 1.8P: When all letters are used, how many different letter arrangements can be made from the letters a.... Problem 1.9P: A child has 12 blocks, of which 6 are black, 4 are red, 1 is white, and 1 is blue. If the child puts... Problem 1.10P: In how many ways can 8 people be seated in a row if a. there are no restrictions on the seating... Problem 1.11P: In how many ways can 3 novels. 2 mathematics books, and 1 chemistry book be arranged on a bookshelf... Problem 1.12P: How many 3 digit numbers zyz, with x, y, z all ranging from 0 to9 have at least 2 of their digits... Problem 1.13P: How many different letter permutations, of any length, can be made using the letters M 0 T T 0. (For... Problem 1.14P: Five separate awards (best scholarship, best leadership qualities, and so on) are to be presented to... Problem 1.15P: Consider a group of 20 people. If everyone shakes hands with everyone else, how many handshakes take... Problem 1.16P: How many 5-card poker hands are there? Problem 1.17P: A dance class consists of 22 students, of which 10 are women and 12 are men. If 5 men and 5 women... Problem 1.18P: A student has to sell 2 books from a collection of 6 math, 7 science, and 4 economics books. How... Problem 1.19P: Seven different gifts are to be distributed among 10 children. How many distinct results are... Problem 1.20P: A committee of 7, consisting of 2 Republicans, 2 Democrats, and 3 Independents, is to be chosen from... Problem 1.21P: From a group of 8 women and 6 men, a committee consisting of 3 men and 3 women is to be formed. How... Problem 1.22P: A person has 8 friends, of whom S will be invited to a party. a. How many choices are there if 2 of... Problem 1.23P: Consider the grid of points shown at the top of the next column. Suppose that, starting at the point... Problem 1.24P: In Problem 23, how many different paths are there from A to B that go through the point circled in... Problem 1.25P: A psychology laboratory conducting dream research contains 3 rooms, with 2 beds in each room. If 3... Problem 1.26P: Show k=0n(nk)2k=3n Simplify k=0n(nk)xk Problem 1.27P: Expand (3x2+y)5. Problem 1.28P: The game of bridge is played by 4 players, each of w1om is dealt 13 cards. How many bridge deals are... Problem 1.29P: Expand (x1+2x2+3x3)4. Problem 1.30P: If 12 people are to be divided into 3 committees of respective sizes 3, 4, and 5, how many divisions... Problem 1.31P: If 8 new teachers are to be divided among 4 schools, how many divisions are possible? What if each... Problem 1.32P: Ten weight lifters are competing in a team weight-lifting contest. Of the lifters, 3 are from the... Problem 1.33P: Delegates from 10 countries, including Russia, France, England, and the United States, are to be... Problem 1.34P: If 8 identical blackboards are to be divided among 4 schools, how many divisions are possible? How... Problem 1.35P: An elevator starts at the basement with 8 people (not including the elevator operator) and... Problem 1.36P: We have 520.000 that must be invested among 4 possible opportunities. Each investment must be... Problem 1.37P: Suppose that 10 fish are caught at a lake that contains 5 distinct types of fish. a. How many... Problem 1.1TE: Prove the generalized version of the basic counting principle. Problem 1.2TE: Two experiments are to be performed. The first can result in any one of m possible outcomes. If the... Problem 1.3TE: In how many ways can r objects be selected from a set of n objects if the order of selection is... Problem 1.4TE: There are (nr) different linear arrangements of n balls of which r are black and nr are white. Give... Problem 1.5TE: Determine the number of vectors (x1,...,xn), such that each x1 is either 0 or 1 andi=1nxiK Problem 1.6TE: How many vectors x1,...,xk are there for which each xi is a positive integer such that1xin and... Problem 1.7TE: Give an analytic proof of Equation (4.1). Problem 1.8TE: Prove that (n+mr)=(n0)(mr)+(n1)(mr1)+...+(nr)(m0) Hint: Consider a group of n men and m women. How... Problem 1.9TE: Use Theoretical Exercise 8 I to prove that (2nn)=k=0n(nk)2 Problem 1.10TE: From a group of n people, suppose that we want to choose a committee of k,kn, one of whom is to be... Problem 1.11TE: The following identity is known as Fermats combinatorial identity:(nk)=i=kn(i1k1)nk Give a... Problem 1.12TE: Consider the following combinatorial identity: k=0nk(nk)=n2n1 a. Present a combinatorial argument... Problem 1.13TE: Show that, for n0 ,i=0n(1)i(ni)=0 Hint: Use the binomial theorem. Problem 1.14TE: From a set of n people, a committee of size j is to be chosen, and from this committee, a... Problem 1.15TE: Let Hn(n) be the number of vectors x1,...,xk for which each xi is a positive integer satisfying 1xin... Problem 1.16TE: Consider a tournament of n contestants in which the outcome is an ordering of these contestants,... Problem 1.17TE: Present a combinatorial explanation of why (nr)=(nr,nr) Problem 1.18TE: Argue that(nn1,n2,...,nr)=(n1n11,n2,...,nr)+(nn1,n21,...,nr)+...+(nn1,n2,...,nr1) Hint: Use an... Problem 1.19TE: Prove the multinomial theorem. Problem 1.20TE: In how many ways can n identical balls be distributed into r urns so that the ith urn contains at... Problem 1.21TE: Argue that there are exactly (rk)(n1nr+k) solutions of x1+x2+...+xr=n for which exactly k of the xi... Problem 1.22TE Problem 1.23TE: Determine the number of vectors (xi,...,xn) such that each xi, is a nonnegative integer and i=1nxik. Problem 1.1STPE: How many different linear arrangements are there of the letters A, B, C, D, E, F for which a. A and... Problem 1.2STPE: If 4 Americans, 3 French people, and 3 British people are to be seated in a row, how many seating... Problem 1.3STPE: A president. treasurer, and secretary. all different, are to be chosen from a club onsisting of 10... Problem 1.4STPE: A student is to answer 7 out of 10 questions in an examination. How many choices has she? How many... Problem 1.5STPE: In how many ways can a man divide 7 gifts among his 3 children if the eldest is to receive 3 gifts... Problem 1.6STPE: How many different 7-place license plates are possible mien 3 of the entries are letters and 4 are... Problem 1.7STPE: Give a combinatorial explanation of the identity(nr)=(nnr) Problem 1.8STPE: Consider n-digit numbers where each digit is one of the 10 integers 0,1, ... ,9. How many such... Problem 1.9STPE: Consider three classes, each consisting of n students. From this group of 3n students, a group of 3... Problem 1.10STPE: How many 5-digit numbers can be formed from the integers 1,2,... ,9 if no digit can appear more than... Problem 1.11STPE: From 10 married couples, we want to select a group of 6 people that is not allowed to contain a... Problem 1.12STPE: A committee of 6 people is to be chosen from a group consisting of 7 men and 8 women. If the... Problem 1.13STPE: An art collection on auction consisted of 4 Dalis, 5 van Goghs. and 6 Picassos, At the auction were... Problem 1.14STPE Problem 1.15STPE: A total of n students are enrolled in a review course for the actuarial examination in probability.... Problem 1.16STPE Problem 1.17STPE: Give an analytic verification of (n2)=(k2)+k(nk)+(n+k2),1kn. Now, give a combinatorial argument for... Problem 1.18STPE: In a certain community, there are 3 families consisting of a single parent and 1 child, 3 families... Problem 1.19STPE: If there are no restrictions on where the digits and letters are placed, how many 8-place license... Problem 1.20STPE: Verify the identityx1+...+xr=n,xi0n!x1!x2!...xr!=rn a. by a combinatorial argument that first notes... Problem 1.21STPE: Simplify n(n2)+(n3)...+(1)n+1(nn) Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
The joint density function of random variables X and Y is given as follows:
Find:
(a) P{Y > 2}
(b) P{1 < X + Y < 3}
Transcribed Image Text: The image represents the joint probability density function (PDF) of two continuous random variables, \(X\) and \(Y\).
The function \( f_{XY}(x, y) \) is defined as follows:
\[
f_{XY}(x, y) =
\begin{cases}
e^{-(x+y)}, & \text{for } x, y > 0 \\
0, & \text{otherwise}
\end{cases}
\]
### Explanation:
- **Function \( e^{-(x+y)} \):** This part of the function applies when both \(x\) and \(y\) are greater than zero. It represents the joint probability density in this region.
- **Zero Otherwise:** The function is zero in the case where either \(x\) or \(y\) are not greater than zero, indicating that there is no probability mass outside the positive quadrant of the xy-plane.
### Context:
This type of function is useful in probabilistic studies and statistical methods for continuous data to understand the likelihood of different combinations of values for \(x\) and \(y\). The exponential decay suggests that higher values of \(x\) and \(y\) are less likely.
Expression, rule, or law that gives the relationship between an independent variable and dependent variable. Some important types of functions are injective function, surjective function, polynomial function, and inverse function.
Expert Solution
Step by step
Solved in 2 steps with 2 images
![The image represents the joint probability density function (PDF) of two continuous random variables, \(X\) and \(Y\).
The function \( f_{XY}(x, y) \) is defined as follows:
\[
f_{XY}(x, y) =
\begin{cases}
e^{-(x+y)}, & \text{for } x, y > 0 \\
0, & \text{otherwise}
\end{cases}
\]
### Explanation:
- **Function \( e^{-(x+y)} \):** This part of the function applies when both \(x\) and \(y\) are greater than zero. It represents the joint probability density in this region.
- **Zero Otherwise:** The function is zero in the case where either \(x\) or \(y\) are not greater than zero, indicating that there is no probability mass outside the positive quadrant of the xy-plane.
### Context:
This type of function is useful in probabilistic studies and statistical methods for continuous data to understand the likelihood of different combinations of values for \(x\) and \(y\). The exponential decay suggests that higher values of \(x\) and \(y\) are less likely.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Faddade67-6dca-41b9-b5d9-3d81c38171e9%2Fad58ba89-2dbd-4255-88b7-86b90d397aa6%2Fk2wz6e_processed.png&w=3840&q=75)