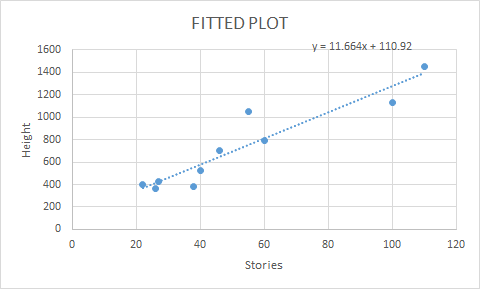
The height (sidewalk to roof) of notable tall buildings in America is compared to the number of stories of the building (beginning at street level). Height (in feet) Stories 1050 55 428 27 362 26 529 40 790 60 401 22 380 38 1454 110 1127 100 700 46 Part (a) Using "stories" as the independent variable and "height" as the dependent variable, make a scatter plot of the data. Part (b) Does it appear from inspection that there is a relationship between the variables? YesNo Part (c) Calculate the least squares line. Put the equation in the form of: ŷ = a + bx. (Round your answers to three decimal places.) ŷ = + x Part (d) Find the correlation coefficient r. (Round your answer to four decimal places.) r = Is it significant? Yes or No ? Part (e) Find the estimated height for 34 stories. (Use your equation from part (c). Round your answer to one decimal place.) ft Find the estimated height for 92 stories. (Use your equation from part (c). Round your answer to one decimal place.) ft Part (f) Use the two points in part (e) to plot the least squares line. (Upload your file below.) Part (g) Based on the above data, is there a linear relationship between the number of stories in tall buildings and the height of the buildings? Yes or No? Part (h) Are there any outliers in the above data? If so, which point(s)? Select one of the following No, there are no outliers. Yes, (55, 1050) and (22, 401) are outliers. Yes, (55, 1050) is an outlier. Yes, (22, 401) is an outlier. Part (i) What is the estimated height of a building with 3 stories? (Use your equation from part (c). Round your answer to one decimal place.) ft Does the least squares line give an accurate estimate of height? Explain why or why not. . The least squares regression line does not give an accurate estimate because the estimated height of a building with three stories is not within the range of y-values in the data. . The estimate for the height of a three-story building does not make sense in this situation. . The least squares regression line does not give an accurate estimate because a three-story building is not within the range of x-values in the data. . The least squares regression line does give an accurate estimate because none of the buildings surveyed had three stories. Part (j) Based on the least squares line, adding an extra story adds about how many feet to a building? (Round your answer to three decimal places.) ft Part (k) What is the slope of the least squares (best-fit) line? (Round your answer to three decimal places.) Interpret the slope. As the (---Select---) of the building increases by one unit, the ( ---Select---) of the building increases by (---Select---) Select from the following height feet number of stories stories

The height (sidewalk to roof) of notable tall buildings in America is compared to the number of stories of the building (beginning at street level). Height (in feet) Stories 1050 55 428 27 362 26 529 40 790 60 401 22 380 38 1454 110 1127 100 700 46 Part (a) Using "stories" as the independent variable and "height" as the dependent variable, make a scatter plot of the data. Part (b) Does it appear from inspection that there is a relationship between the variables? YesNo Part (c) Calculate the least squares line. Put the equation in the form of: ŷ = a + bx. (Round your answers to three decimal places.) ŷ = + x Part (d) Find the correlation coefficient r. (Round your answer to four decimal places.) r = Is it significant? Yes or No ? Part (e) Find the estimated height for 34 stories. (Use your equation from part (c). Round your answer to one decimal place.) ft Find the estimated height for 92 stories. (Use your equation from part (c). Round your answer to one decimal place.) ft Part (f) Use the two points in part (e) to plot the least squares line. (Upload your file below.) Part (g) Based on the above data, is there a linear relationship between the number of stories in tall buildings and the height of the buildings? Yes or No? Part (h) Are there any outliers in the above data? If so, which point(s)? Select one of the following No, there are no outliers. Yes, (55, 1050) and (22, 401) are outliers. Yes, (55, 1050) is an outlier. Yes, (22, 401) is an outlier. Part (i) What is the estimated height of a building with 3 stories? (Use your equation from part (c). Round your answer to one decimal place.) ft Does the least squares line give an accurate estimate of height? Explain why or why not. . The least squares regression line does not give an accurate estimate because the estimated height of a building with three stories is not within the range of y-values in the data. . The estimate for the height of a three-story building does not make sense in this situation. . The least squares regression line does not give an accurate estimate because a three-story building is not within the range of x-values in the data. . The least squares regression line does give an accurate estimate because none of the buildings surveyed had three stories. Part (j) Based on the least squares line, adding an extra story adds about how many feet to a building? (Round your answer to three decimal places.) ft Part (k) What is the slope of the least squares (best-fit) line? (Round your answer to three decimal places.) Interpret the slope. As the (---Select---) of the building increases by one unit, the ( ---Select---) of the building increases by (---Select---) Select from the following height feet number of stories stories

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Concept explainers

Question

The height (sidewalk to roof) of notable tall buildings in America is compared to the number of stories of the building (beginning at street level).

Height (in feet)	Stories
1050	55
428	27
362	26
529	40
790	60
401	22
380	38
1454	110
1127	100
700	46

Part (a)
Using "stories" as the independent variable and "height" as the dependent variable, make a scatter plot of the data.
- Part (b)
  
  Does it appear from inspection that there is a relationship between the variables?
  YesNo
- Part (c)
  
  Calculate the least squares line. Put the equation in the form of:
  ŷ = a + bx.
  (Round your answers to three decimal places.)
  ŷ = + x
- Part (d)
  
  Find the correlation coefficient r. (Round your answer to four decimal places.)
  r =
  
  Is it significant?
  Yes or No ?
- Part (e)
  
  Find the estimated height for 34 stories. (Use your equation from part (c). Round your answer to one decimal place.)
  ft
  
  Find the estimated height for 92 stories. (Use your equation from part (c). Round your answer to one decimal place.)
  ft
- Part (f)
  
  Use the two points in part (e) to plot the least squares line. (Upload your file below.)
- Part (g)
  
  Based on the above data, is there a linear relationship between the number of stories in tall buildings and the height of the buildings?
  Yes or No?
- Part (h)
  
  Are there any outliers in the above data? If so, which point(s)? Select one of the following
  No, there are no outliers.
  
  Yes, (55, 1050) and (22, 401) are outliers.
  
  Yes, (55, 1050) is an outlier.
  
  Yes, (22, 401) is an outlier.
- Part (i)
  
  What is the estimated height of a building with 3 stories? (Use your equation from part (c). Round your answer to one decimal place.)
  ft
  
  Does the least squares line give an accurate estimate of height? Explain why or why not.
  
  . The least squares regression line does not give an accurate estimate because the estimated height of a building with three stories is not within the range of y-values in the data.
  
  . The estimate for the height of a three-story building does not make sense in this situation.
  
  . The least squares regression line does not give an accurate estimate because a three-story building is not within the range of x-values in the data.
  
  . The least squares regression line does give an accurate estimate because none of the buildings surveyed had three stories.
- Part (j)
  
  Based on the least squares line, adding an extra story adds about how many feet to a building? (Round your answer to three decimal places.)
  ft
- Part (k)
  
  What is the slope of the least squares (best-fit) line? (Round your answer to three decimal places.)
  
  Interpret the slope.
  As the (---Select---) of the building increases by one unit, the ( ---Select---) of the building increases by (---Select---)
  
  Select from the following
  
  height
  
  feet
  
  number of stories
  
  stories

Expert Solution

Step 1

Hey, since there are multiple subparts posted, we will answer first three subparts. If you want any specific subpart to be answered then please submit that subpart only or specify the subpart in your message.

Step-by-step procedure to draw the fitted line plot using Excel:

In Excel sheet, enter and select Height in one column and enter Stories in one column.
In Insert, select Scatter with only markers under Scatter.
Right click the points in the graph and select Add trend line.
Select Linear in Trend/Regression Type.
Click Display Equation.
Click Ok.

Output obtained using Excel is given below:

Trending now

This is a popular solution!

Step by step

Solved in 2 steps with 1 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Correlation, Regression, and Association$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.