The graphs of f and g are given. Use them to evaluate each limit, if it exists. If the limit does not exist, explain why. YA y = f(x) 1 1 (i) lim [f(x) + g(x)] x 2 (ii) lim [f(x) + g(x)] x→1 x y y = g(x) A 1 0 1 X (iii) lim f(x)g(x) x →0 f(x) x→-1 g(x) (iv) lim (v) lim [x³ f(x)] 7← (vi) lim √3+ f(x) x-1
The graphs of f and g are given. Use them to evaluate each limit, if it exists. If the limit does not exist, explain why. YA y = f(x) 1 1 (i) lim [f(x) + g(x)] x 2 (ii) lim [f(x) + g(x)] x→1 x y y = g(x) A 1 0 1 X (iii) lim f(x)g(x) x →0 f(x) x→-1 g(x) (iv) lim (v) lim [x³ f(x)] 7← (vi) lim √3+ f(x) x-1
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![The graphs of \( f \) and \( g \) are given. Use them to evaluate each limit, if it exists. If the limit does not exist, explain why.
**Graph 1: \( y = f(x) \)**
- The graph is a piecewise curve.
- At \( x = 1 \), there is an open circle at \( y = 2 \), indicating that \( f(1) \) is not defined, but as \( x \) approaches 1 from either direction, \( f(x) \) approaches 2.
- The graph generally increases with some variation.
**Graph 2: \( y = g(x) \)**
- The graph is another piecewise curve.
- At \( x = 0 \), there is an open circle at \( y = 1 \), indicating a discontinuity, but as \( x \) approaches 0, \( g(x) \) approaches 1.
- The graph shows an arc-like increase and decrease.
**Limits to Evaluate:**
(i) \(\lim_{x \to 2} [f(x) + g(x)]\)
(ii) \(\lim_{x \to 1} [f(x) + g(x)]\)
(iii) \(\lim_{x \to 0} f(x)g(x)\)
(iv) \(\lim_{x \to -1} \frac{f(x)}{g(x)}\)
(v) \(\lim_{x \to 2} [x^3 f(x)]\)
(vi) \(\lim_{x \to 1} \sqrt{3 + f(x)}\)
To evaluate these limits, analyze each graph around the specified values and apply limit properties. If a function approaches different values from left and right at a point, the limit at that point does not exist.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc87785b0-7b08-4187-be5d-f53b11d0a1a0%2Fb192af4d-b78b-47c8-9103-d37f16e1a288%2F578thv_processed.png&w=3840&q=75)
Transcribed Image Text:The graphs of \( f \) and \( g \) are given. Use them to evaluate each limit, if it exists. If the limit does not exist, explain why.
**Graph 1: \( y = f(x) \)**
- The graph is a piecewise curve.
- At \( x = 1 \), there is an open circle at \( y = 2 \), indicating that \( f(1) \) is not defined, but as \( x \) approaches 1 from either direction, \( f(x) \) approaches 2.
- The graph generally increases with some variation.
**Graph 2: \( y = g(x) \)**
- The graph is another piecewise curve.
- At \( x = 0 \), there is an open circle at \( y = 1 \), indicating a discontinuity, but as \( x \) approaches 0, \( g(x) \) approaches 1.
- The graph shows an arc-like increase and decrease.
**Limits to Evaluate:**
(i) \(\lim_{x \to 2} [f(x) + g(x)]\)
(ii) \(\lim_{x \to 1} [f(x) + g(x)]\)
(iii) \(\lim_{x \to 0} f(x)g(x)\)
(iv) \(\lim_{x \to -1} \frac{f(x)}{g(x)}\)
(v) \(\lim_{x \to 2} [x^3 f(x)]\)
(vi) \(\lim_{x \to 1} \sqrt{3 + f(x)}\)
To evaluate these limits, analyze each graph around the specified values and apply limit properties. If a function approaches different values from left and right at a point, the limit at that point does not exist.
Expert Solution
Step 1
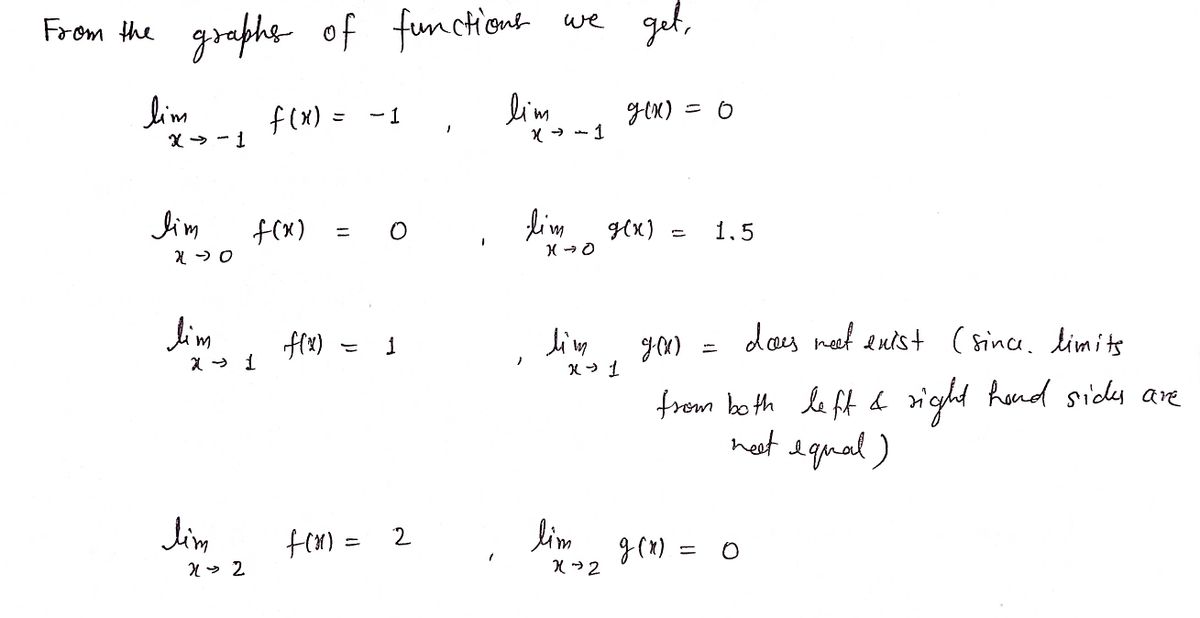
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

