The function g(x) is a transformation of the function f(x) = 3. The coordinate plane shows the graph of both functions. <-8 -6 -4 -2 0 ((0.1) (29) (1.3) 2 Ax)=3* (2, 0) 4 6
The function g(x) is a transformation of the function f(x) = 3. The coordinate plane shows the graph of both functions. <-8 -6 -4 -2 0 ((0.1) (29) (1.3) 2 Ax)=3* (2, 0) 4 6
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question

Transcribed Image Text:Based on your knowledge of transformations, which of the equations represents the graph of \( g(x) \)?
a. \( g(x) = 3^{x-2} - 1 \)
b. \( g(x) = -3^{x+2} + 1 \)
c. \( g(x) = -3^{x-2} + 1 \)
d. \( g(x) = 3^{x+2} - 1 \)

Transcribed Image Text:The function \( g(x) \) is a transformation of the function \( f(x) = 3^x \). The coordinate plane shows the graph of both functions.
### Description of the Graph:
1. **Axes and Quadrants:**
- The graph displays a coordinate plane with an x-axis and y-axis intersecting at the origin (0,0).
2. **Functions:**
- The graph includes two different curves representing the functions \( f(x) = 3^x \) and \( g(x) \).
3. **Color Coding:**
- The graph of \( f(x) = 3^x \) is shown in maroon.
- The graph of \( g(x) \) is shown in teal.
4. **Labeled Points:**
- On the maroon graph (\( f(x) \)):
- (0, 1)
- (1, 3)
- (2, 9)
- On the teal graph (\( g(x) \)):
- (0, 1)
- (2, 0)
- (3, -2)
- (4, -8)
5. **Behavior:**
- The maroon curve (\( f(x) = 3^x \)) shows exponential growth as it moves from left to right.
- The teal curve (\( g(x) \)) shows a different behavior, potentially involving a reflection or shift, altering its path significantly from \( f(x) \).
This graph effectively contrasts the original function \( f(x) = 3^x \) with its transformation in \( g(x) \), illustrating their different growth patterns and point transformations.
Expert Solution
Step 1
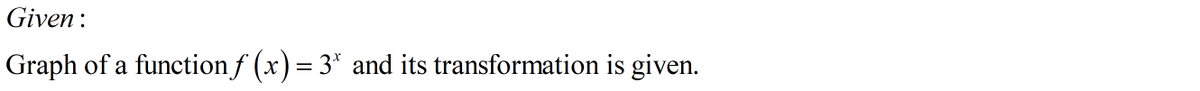
Step by step
Solved in 2 steps with 3 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education