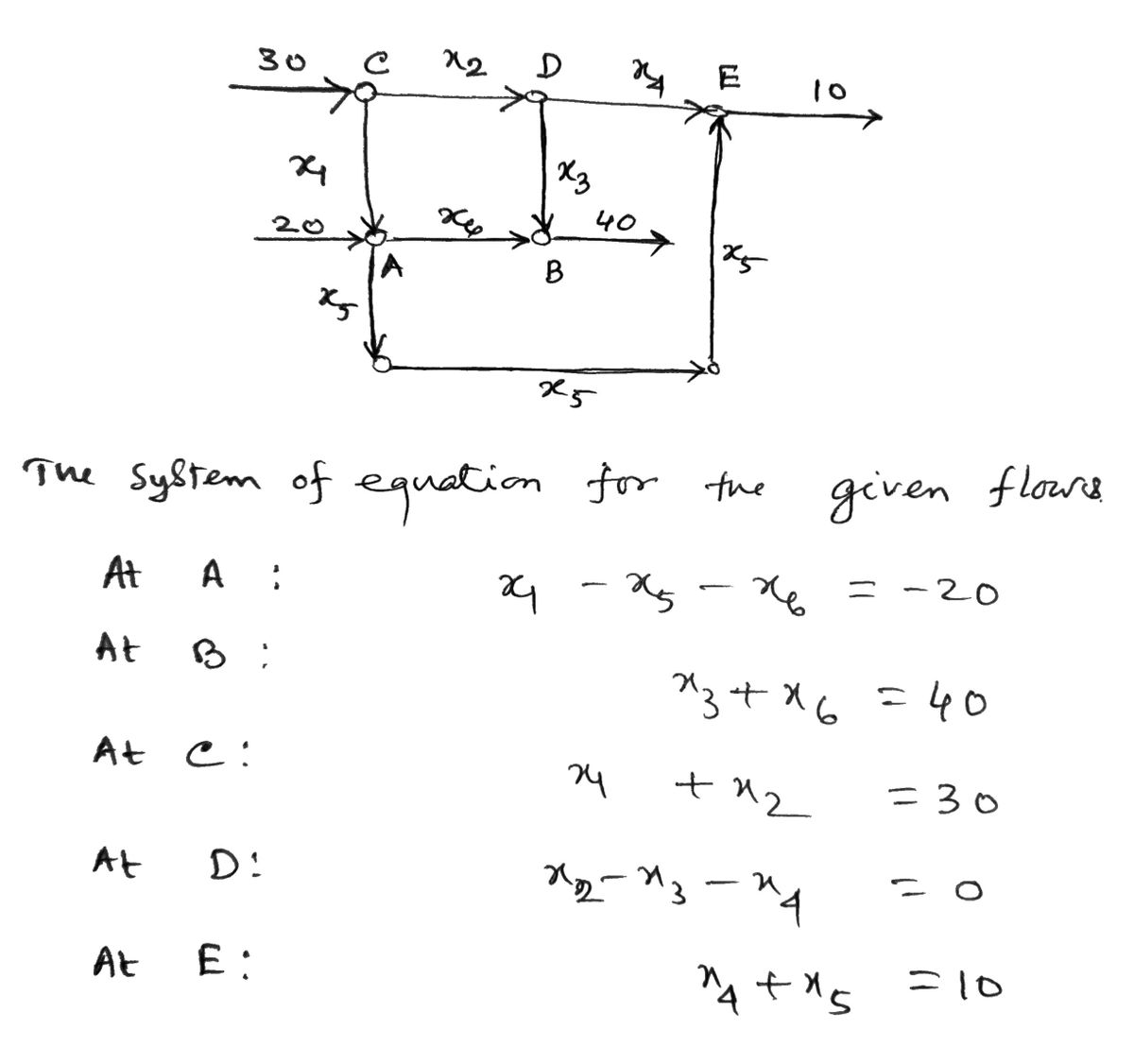
The following picture represents a network of interconnected pipelines. The arrows represent the flow measured by ft³ per minutes. The values above the arrows represent the flow in the given segment, the flow is regulated by the valves at the intersections. Of course the amount of water per minute entering each connection, has to be equal to the amount of water exiting the connection. This leads to five equations. 30 D 10 I3 20 40 A B 25 1. Write dowm the system of linear equations that represents the flow at each relevant valve. 2. Find the augmented matrix and its row reduced echelon form. 3. How many solutions are there? Notice that the valves allow only one direction for the flow. This means that we require each x; not to be negative. A solution with all positive x; is called feasible. 4. Express all the feasible solutions in terms of inequalities. 5. Suppose you will need to repair the pipe between connections A and B, you will want to have the flow between A and B as minimal as possible. What is the minimal value of x6 to have a feasible solution. 6. Using what you found in the previous answer write all the values of xi, for i = 1,..., 6 and make sure they are a solution of your system. 7. What happens if you reverse the flow in the segment BD (by substituting the valve)? Find the minimal value of x6 that gives you a feasible solution.
The following picture represents a network of interconnected pipelines. The arrows represent the flow measured by ft³ per minutes. The values above the arrows represent the flow in the given segment, the flow is regulated by the valves at the intersections. Of course the amount of water per minute entering each connection, has to be equal to the amount of water exiting the connection. This leads to five equations. 30 D 10 I3 20 40 A B 25 1. Write dowm the system of linear equations that represents the flow at each relevant valve. 2. Find the augmented matrix and its row reduced echelon form. 3. How many solutions are there? Notice that the valves allow only one direction for the flow. This means that we require each x; not to be negative. A solution with all positive x; is called feasible. 4. Express all the feasible solutions in terms of inequalities. 5. Suppose you will need to repair the pipe between connections A and B, you will want to have the flow between A and B as minimal as possible. What is the minimal value of x6 to have a feasible solution. 6. Using what you found in the previous answer write all the values of xi, for i = 1,..., 6 and make sure they are a solution of your system. 7. What happens if you reverse the flow in the segment BD (by substituting the valve)? Find the minimal value of x6 that gives you a feasible solution.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Based on the answers from questions 1,2, and 3. Please please help with question 5,6,7. At least answer one of them if not all.

Transcribed Image Text:Then the Syaiam of egnalims
E 10
4-, -* -20
"+, = 40
|O e agmanted maliie je
At tme junclion *
Entexing ament = x + 20
Exiting amomt - *+
-11-20
0, 30
X +20 =* +
LaoD 11
4- - x - -20
The augmanta ulin
At te janclionA
Entering = x3tKg
amout
ament
1: 40
0100
OD1 - 1
I 50
Exiting!
*3+ , = 40
At tne junctione
Entering
ameuf
amonl
= 30
%3D
* * - - I 20
Exiting
" amomt
30 - + ng
- 1-4
1 150
1:40
| 2 60
At
the fun ctan D
Enterig amnt = 72
Exiting amomt
* = y + 4
2 - 3 - , = O
- Kg +
-| |-10
M3 -
0 01
1 y
2
1 2 10.
At femetion E
Entering am omt
Exiting amant =I0
*4 +* = 10.
!-20
40
-1
-2
-60
35
R, +Rs.
! 15
• IS
40
1
-I
-25
35
This a
reduced eehelam frrm.
tre vEw
2 = 15
3 + = 40
> 3 = 4e -
4 - 4 = -2
* + = 35 Xs = 3s-
* > = -25
Smea
40 - 0 € Yo
* -25 >0 =) *> 25
35 - 4 >o 2 4 < 35
Thus Solution
is
/15
+ *6
wwre
25 4 63S
40
-
-25
The feerisle Llution
25 < < 3s
35
Tuere are nfiute
solutions,

Transcribed Image Text:The following picture represents a network of interconnected pipelines. The arrows represent the flow
measured by ft³ per minutes. The values above the arrows represent the flow in the given segment,
the flow is regulated by the valves at the intersections.
Of course the amount of water per minute entering each connection, has to be equal to the amount of
water exiting the connection. This leads to five equations.
30
D
10
23
20
40
B
15
1. Write down the system of linear equations that represents the flow at each relevant valve.
2. Find the augmented matrix and its row reduced echelon form.
3. How many solutions are there? Notice that the valves allow only one direction for the flow.
This means that we require each x; not to be negative. A solution with all positive x; is called
feasible.
4. Express all the feasible solutions in terms of inequalities.
5. Suppose you will need to repair the pipe between connections A and B, you will want to have
the flow between A and B as minimal as possible. What is the minimal value of x6 to have a
feasible solution.
6. Using what you found in the previous answer write all the values of xi, for i = 1, ..., 6 and make
sure they are a solution of your system.
7. What happens if you reverse the flow in the segment BD (by substituting the valve)? Find the
minimal value of x6 that gives you a feasible solution.
Expert Solution
Step 1
Step by step
Solved in 7 steps with 6 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

