The following information is known regarding the events A, B, and C: • P(A) = 0.2, P(B) = 0.3, P(C) = 0.4 • P(A Intersect B) = 0.06, P(A Intersect C) = 0.08, P(B Intersect C) = 0.12 • P(A Intersect B Intersect C) = 0.03 1) Are the events B and C independent? Why or why not? 2) What is the probability that A occurs or B does not occur?
The following information is known regarding the
• P(A) = 0.2, P(B) = 0.3, P(C) = 0.4
• P(A Intersect B) = 0.06, P(A Intersect C) = 0.08, P(B Intersect C) = 0.12
• P(A Intersect B Intersect C) = 0.03
1) Are the events B and C independent? Why or why not?
2) What is the
1)
From the given information, P(A) = 0.2, P(B) = 0.3, P(C) = 0.4, P(A Intersect B) = 0.06, P(A Intersect C) = 0.08, P(B Intersect C) = 0.12, P(A Intersect B Intersect C) = 0.03
The required value P (B|C) is obtained below:

Thus, the value of P (B|C)is 0.3.
If the condition of events B and C are independent,
P (B|C) = P(B)
Then, the value of P (B|C) = 0.3 and P(B) =0.3
Here,
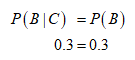
Hence, the events B and C are independent.
Step by step
Solved in 2 steps with 4 images




