The following graph corresponds to f'(x), the first derivative of f(x). If the graph does not appear, please reload the page. 1000 500 4 2 -500- Enter the number of critical points/numbers of f(x): Enter the number of relative maxima of f(x): Enter the number of relative minima of f(x): -1000 Based on the above graph of the derivative of f(x), determine the number critical points and relative extrema of f(x). You may assume that f'(x) is continuous, f'(x) is defined for all x, and f'(x) = 0 only when x = -4, x = 0, and x = 4.
The following graph corresponds to f'(x), the first derivative of f(x). If the graph does not appear, please reload the page. 1000 500 4 2 -500- Enter the number of critical points/numbers of f(x): Enter the number of relative maxima of f(x): Enter the number of relative minima of f(x): -1000 Based on the above graph of the derivative of f(x), determine the number critical points and relative extrema of f(x). You may assume that f'(x) is continuous, f'(x) is defined for all x, and f'(x) = 0 only when x = -4, x = 0, and x = 4.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
![The following graph corresponds to \( f'(x) \), the first derivative of \( f(x) \). If the graph does not appear, please reload the page.
*Graph Description:*
The graph shows the plot of a continuous function \( f'(x) \) against \( x \). Key points include:
- The x-axis is labeled with values approximately at \( -4, -2, 0, 2, \) and \( 4 \).
- The y-axis includes values ranging from \(-1000\) to \(1000\).
- The curve starts above \( y = 1000 \), decreases sharply, and crosses the x-axis near \( x = -4 \).
- It continues downward, reaching a minimum near \(-1000\) before increasing again and crossing the x-axis near \( x = 0 \).
- It peaks at a point between \( x = 2 \) and \( x = 3 \), then declines and crosses the x-axis at \( x = 4 \).
- Finally, the curve decreases significantly.
*Instructions:*
Based on the above graph of the derivative of \( f(x) \), determine the number of critical points and relative extrema of \( f(x) \). You may assume that \( f'(x) \) is continuous, \( f'(x) \) is defined for all \( x \), and \( f'(x) = 0 \) only when \( x = -4, x = 0, \) and \( x = 4 \).
- Enter the number of critical points/numbers of \( f(x) \): [ ]
- Enter the number of relative maxima of \( f(x) \): [ ]
- Enter the number of relative minima of \( f(x) \): [ ]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F11ff9f03-4cfd-4604-9eab-3af23331f424%2Fb45ff166-924a-4ba2-a1fa-1d1467a63827%2Fgtst8mr_processed.png&w=3840&q=75)
Transcribed Image Text:The following graph corresponds to \( f'(x) \), the first derivative of \( f(x) \). If the graph does not appear, please reload the page.
*Graph Description:*
The graph shows the plot of a continuous function \( f'(x) \) against \( x \). Key points include:
- The x-axis is labeled with values approximately at \( -4, -2, 0, 2, \) and \( 4 \).
- The y-axis includes values ranging from \(-1000\) to \(1000\).
- The curve starts above \( y = 1000 \), decreases sharply, and crosses the x-axis near \( x = -4 \).
- It continues downward, reaching a minimum near \(-1000\) before increasing again and crossing the x-axis near \( x = 0 \).
- It peaks at a point between \( x = 2 \) and \( x = 3 \), then declines and crosses the x-axis at \( x = 4 \).
- Finally, the curve decreases significantly.
*Instructions:*
Based on the above graph of the derivative of \( f(x) \), determine the number of critical points and relative extrema of \( f(x) \). You may assume that \( f'(x) \) is continuous, \( f'(x) \) is defined for all \( x \), and \( f'(x) = 0 \) only when \( x = -4, x = 0, \) and \( x = 4 \).
- Enter the number of critical points/numbers of \( f(x) \): [ ]
- Enter the number of relative maxima of \( f(x) \): [ ]
- Enter the number of relative minima of \( f(x) \): [ ]
Expert Solution
Step 1
We know that f(x) will have critical point where
f'(x) = 0
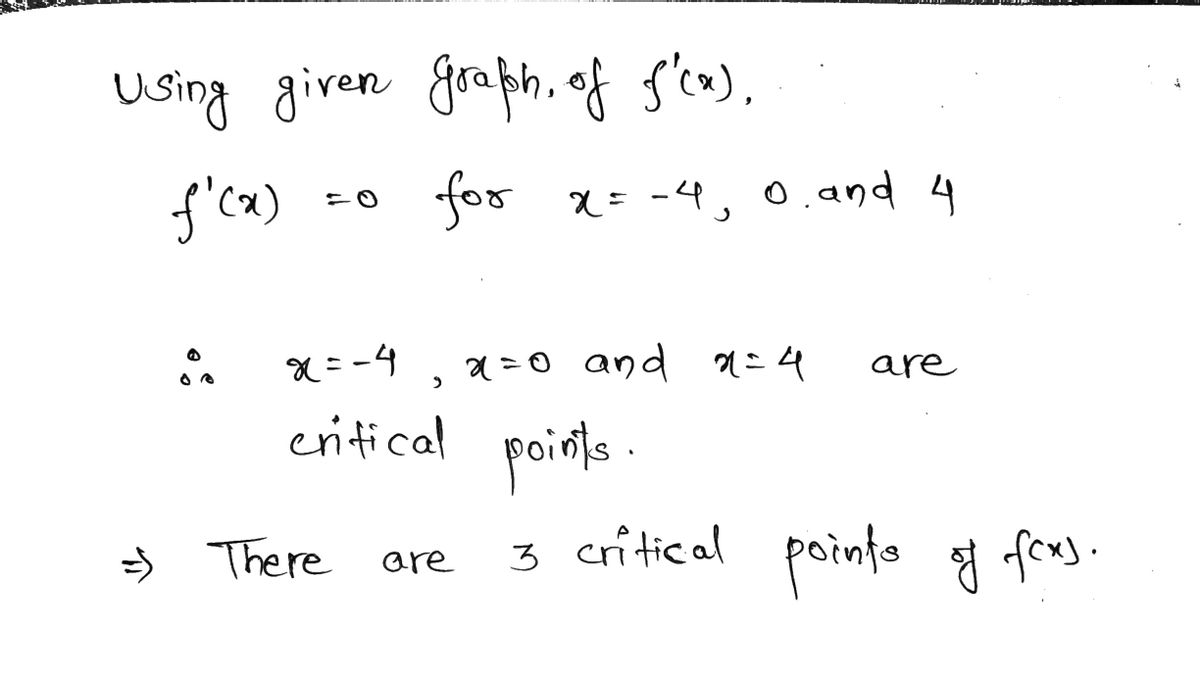
Step by step
Solved in 5 steps with 5 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

