The director of library services at a college did a survey of types of books (by subject) in the circulation library. Then she used library records to take a random sample of 888 books checked out last term and classified the books in the sample by subject. The results are shown below. Subject Area Percent of Books on Subject in Circulation Library on This Subject Number of Books in Sample on This Subject Business 32% 267 Humanities 25% 217 Natural Science 20% 222 Social Science 15% 109 All other subjects 8% 73 Using a 5% level of significance, test the claim that the subject distribution of books in the library fits the distribution of books checked out by students. (a) What is the level of significance? State the null and alternate hypotheses. H0: The distributions are different. H1: The distributions are the same.H0: The distributions are the same. H1: The distributions are different. H0: The distributions are the same. H1: The distributions are the same.H0: The distributions are different. H1: The distributions are different. (b) Find the value of the chi-square statistic for the sample. (Round the expected frequencies to three decimal places. Round the test statistic to three decimal places.) Are all the expected frequencies greater than 5? Yes/No What sampling distribution will you use? chi-square uniform binomial Student's t normal What are the degrees of freedom? (c) Estimate the P-value of the sample test statistic. A. P-value > 0.100 B. 0.050 < P-value < 0.100 C. 0.025 < P-value < 0.050 D. 0.010 < P-value < 0.025 E. 0.005 < P-value < 0.010 F. P-value < 0.005 (d) Based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis of independence? A. Since the P-value > α, we fail to reject the null hypothesis. B. Since the P-value > α, we reject the null hypothesis. C. Since the P-value ≤ α, we reject the null hypothesis. D. Since the P-value ≤ α, we fail to reject the null hypothesis. (e) Interpret your conclusion in the context of the application. A. At the 5% level of significance, the evidence is sufficient to conclude that the subject distribution of books in the library is different from that of books checked out by students. B. At the 5% level of significance, the evidence is insufficient to conclude that the subject distribution of books in the library is different from that of books checked out by students.

The director of library services at a college did a survey of types of books (by subject) in the circulation library. Then she used library records to take a random sample of 888 books checked out last term and classified the books in the sample by subject. The results are shown below. Subject Area Percent of Books on Subject in Circulation Library on This Subject Number of Books in Sample on This Subject Business 32% 267 Humanities 25% 217 Natural Science 20% 222 Social Science 15% 109 All other subjects 8% 73 Using a 5% level of significance, test the claim that the subject distribution of books in the library fits the distribution of books checked out by students. (a) What is the level of significance? State the null and alternate hypotheses. H0: The distributions are different. H1: The distributions are the same.H0: The distributions are the same. H1: The distributions are different. H0: The distributions are the same. H1: The distributions are the same.H0: The distributions are different. H1: The distributions are different. (b) Find the value of the chi-square statistic for the sample. (Round the expected frequencies to three decimal places. Round the test statistic to three decimal places.) Are all the expected frequencies greater than 5? Yes/No What sampling distribution will you use? chi-square uniform binomial Student's t normal What are the degrees of freedom? (c) Estimate the P-value of the sample test statistic. A. P-value > 0.100 B. 0.050 < P-value < 0.100 C. 0.025 < P-value < 0.050 D. 0.010 < P-value < 0.025 E. 0.005 < P-value < 0.010 F. P-value < 0.005 (d) Based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis of independence? A. Since the P-value > α, we fail to reject the null hypothesis. B. Since the P-value > α, we reject the null hypothesis. C. Since the P-value ≤ α, we reject the null hypothesis. D. Since the P-value ≤ α, we fail to reject the null hypothesis. (e) Interpret your conclusion in the context of the application. A. At the 5% level of significance, the evidence is sufficient to conclude that the subject distribution of books in the library is different from that of books checked out by students. B. At the 5% level of significance, the evidence is insufficient to conclude that the subject distribution of books in the library is different from that of books checked out by students.

Name: The director of library services at a college did a survey of types of
Uploaded: 2024-03-20T07:06:27.000Z
Channel: Bartleby
Description: The director of library services at a college did a survey of types of books (by subject) in the circulation library. Then she used library records to take a random sample of 888 books checked out last term and classified the books in the sample by s

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Concept explainers

Topic Video

Question

Subject Area	Percent of Books on Subject in Circulation Library on This Subject	Number of Books in Sample on This Subject
Business	32%	267
Humanities	25%	217
Natural Science	20%	222
Social Science	15%	109
All other subjects	8%	73

Using a 5% level of significance, test the claim that the subject distribution of books in the library fits the distribution of books checked out by students.

(a) What is the level of significance?

State the null and alternate hypotheses.

H₀: The distributions are different.
H₁: The distributions are the same.H₀: The distributions are the same.
H₁: The distributions are different. H₀: The distributions are the same.
H₁: The distributions are the same.H₀: The distributions are different.
H₁: The distributions are different.

(b) Find the value of the chi-square statistic for the sample. (Round the expected frequencies to three decimal places. Round the test statistic to three decimal places.)

Are all the expected frequencies greater than 5?

Yes/No

What sampling distribution will you use?

chi-square

uniform

binomial

Student's t

normal

What are the degrees of freedom?

(c) Estimate the P-value of the sample test statistic.

A. P-value > 0.100

B. 0.050 < P-value < 0.100

C. 0.025 < P-value < 0.050

D. 0.010 < P-value < 0.025

E. 0.005 < P-value < 0.010

F. P-value < 0.005

(d) Based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis of independence?

A. Since the P-value > α, we fail to reject the null hypothesis.

B. Since the P-value > α, we reject the null hypothesis.

C. Since the P-value ≤ α, we reject the null hypothesis.

D. Since the P-value ≤ α, we fail to reject the null hypothesis.

(e) Interpret your conclusion in the context of the application.

A. At the 5% level of significance, the evidence is sufficient to conclude that the subject distribution of books in the library is different from that of books checked out by students.

B. At the 5% level of significance, the evidence is insufficient to conclude that the subject distribution of books in the library is different from that of books checked out by students.

Expert Solution

Step 1

(a)

Determine the level of significance.

Significance level:

In order to decide how small the p-value should be for providing convincing evidence against the null hypothesis, a value should be used. The value that is used as the rule or the criterion for deciding how small the p-value should be is called as level of significance.

Null hypothesis:

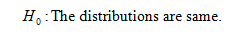
Alternative hypothesis:

Correct option: Option 2

Step by step

Solved in 4 steps with 11 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Data Collection, Sampling Methods, and Bias$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.