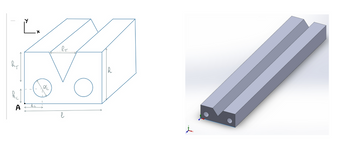
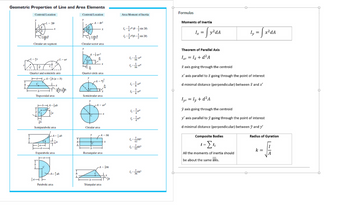
Find the moment of inertia and radius of gyration of the section of this bar about an axis parallel to x-axis going through the center of gravity of the bar. The bar is symmetrical about the axis parallel to y-axis and going through the center of gravity of the bar and about the axis parallel to z-axis and going through the center of gravity of the bar. The dimensions of the section are: l=55 mm, h=22 mm The triangle: hT=12 mm, lT=19 mm and the 2 circles: diameter=8 mm, hC=6 mm, dC=8 mm. A is the origin of the referential axis. Provide an organized table and explain all your steps to find the moment of inertia and radius of gyration about an axis parallel to x-axis and going through the center of gravity of the bar. Does the radius of gyration make sense? Enter the y position of the center of gravity of the bar in mm with one decimal.
Find the moment of inertia and radius of gyration of the section of this bar about an axis parallel to x-axis going through the center of gravity of the bar.
The bar is symmetrical about the axis parallel to y-axis and going through the center of gravity of the bar and about the axis parallel to z-axis and going through the center of gravity of the bar.
The dimensions of the section are:
- l=55 mm, h=22 mm
- The triangle: hT=12 mm, lT=19 mm
- and the 2 circles: diameter=8 mm, hC=6 mm, dC=8 mm.
A is the origin of the referential axis.
Provide an organized table and explain all your steps to find the moment of inertia and radius of gyration about an axis parallel to x-axis and going through the center of gravity of the bar.
Does the radius of gyration make sense?
Enter the y position of the center of gravity of the bar in mm with one decimal.


Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

I am sorry but your values when plugging in are not the correct values. Not too sure where your values are from but can you please redo the question using the given values in this problem and not from a different problem please? (example, height is not 29, it is 22) all values do not correlate to this problem. I was also told when finding the area of triangle to use (1/2)*b*h*Ad^2 and not 1/36*b*h*Ad^2
Find the moment of inertia and radius of gyration of the section of this bar about an axis parallel to x-axis going through the center of gravity of the bar.
The bar is symmetrical about the axis parallel to y-axis and going through the center of gravity of the bar and about the axis parallel to z-axis and going through the center of gravity of the bar.
The dimensions of the section are:
- l=55 mm, h=22 mm
- The triangle: hT=12 mm, lT=19 mm
- and the 2 circles: diameter=8 mm, hC=6 mm, dC=8 mm.
A is the origin of the referential axis.
Provide an organized table and explain all your steps to find the moment of inertia and radius of gyration about an axis parallel to x-axis and going through the center of gravity of the bar.
Does the radius of gyration make sense?
Enter the y position of the center of gravity of the bar in mm with one decimal.