The density of a spherical solid at a point P = (x, y, z) is given by f(x, y, z) = c(x² + y² + z²) , c it is a positive constant. When attempting a displacement from the point P = (1,2,3) of the interior of this solid, according to the vector below: a = (1, 1/2, -1) The density trend is: A) decrease B) increase to the maximum C) keep constant D) decrease to the maximum E) increase
The density of a spherical solid at a point P = (x, y, z) is given by f(x, y, z) = c(x² + y² + z²) , c it is a positive constant. When attempting a displacement from the point P = (1,2,3) of the interior of this solid, according to the vector below:
a = (1, 1/2, -1)
The density trend is:
| A) |
decrease |
| B) |
increase to the maximum |
| C) |
keep constant |
| D) |
decrease to the maximum |
| E) |
increase |
The density of spherical solid at any point P(x,y,z) is given by,
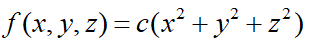
Therefore, the density at point P(1,2,3) is,
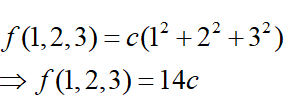
The vector from point A(x1,y1,z1 ) to vector B(x2,y2,z2) is given by,
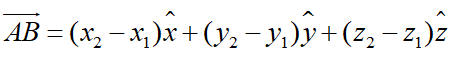
The displacement is from point P(1,2,3) to some point say P'(x2,y2,z2) along the vector a(1,1/2,-1), then,
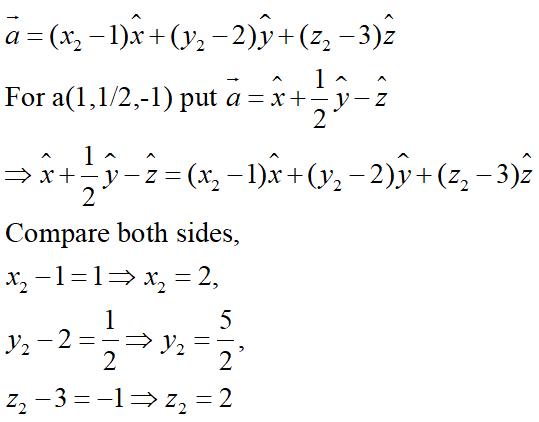
The new location after displacement along vector a is P'(2,5/2,2).
Step by step
Solved in 4 steps with 6 images
