The data table contains waiting times of customers at a bank, where customers enter a single waiting line that feeds three teller windows. Test the claim that the standard deviation of waiting times is less than 1.1 minutes, which is the standard deviation of waiting times at the same bank when separate waiting lines are used at each teller window. Use a significance level of 0.01. Assume that the sample is a simple random sample selected from a normally distributed population. Complete parts (a) through (d) below. Click on the icon to view the data. a. Identify the null and alternative hypotheses. Choose the correct answer below. OA. Ho: <1.1 minutes B. Ho: 1.1 minutes H-11 minutos H 1 1 minutos
The data table contains waiting times of customers at a bank, where customers enter a single waiting line that feeds three teller windows. Test the claim that the standard deviation of waiting times is less than 1.1 minutes, which is the standard deviation of waiting times at the same bank when separate waiting lines are used at each teller window. Use a significance level of 0.01. Assume that the sample is a simple random sample selected from a normally distributed population. Complete parts (a) through (d) below. Click on the icon to view the data. a. Identify the null and alternative hypotheses. Choose the correct answer below. OA. Ho: <1.1 minutes B. Ho: 1.1 minutes H-11 minutos H 1 1 minutos
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question

Transcribed Image Text:The data table contains waiting times of customers at a bank, where customers enter a single waiting line that feeds
three teller windows. Test the claim that the standard deviation of waiting times is less than 1.1 minutes, which is the
standard deviation of waiting times at the same bank when separate waiting lines are used at each teller window. Use
a significance level of 0.01. Assume that the sample is a simple random sample selected from a normally distributed
population. Complete parts (a) through (d) below.
Click on the icon to view the data.
a. Identify the null and alternative hypotheses. Choose the correct answer below.
O A. Ho: <1.1 minutes
B. Ho: 1.1 minutes
HA: 0= 1.1 minutes
HA: G < 1.1 minutes
O C. Ho: 21.1 minutes
HA: < 1.1 minutes
b. Compute the test statistic.
x²=0
(Round to two decimal places as needed.)
O D. Ho: = 1.1 minutes
HA: #1.1 minutes
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
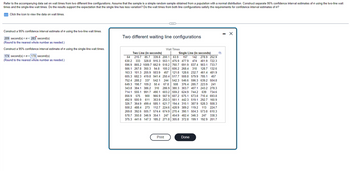
Transcribed Image Text:Refer to the accompanying data set on wait times from two different line configurations. Assume that the sample is a simple random sample obtained from a population with a normal distribution. Construct separate 95% confidence interval estimates of using the two-line wait
times and the single-line wait times. Do the results support the expectation that the single line has less variation? Do the wait times from both line configurations satisfy the requirements for confidence interval estimates of o?
Click the icon to view the data on wait times.
Construct a 95% confidence interval estimate of using the two-line wait times.
209 second(s) << 283 second(s)
(Round to the nearest whole number as needed.)
Construct a 95% confidence interval estimate of using the single-line wait times.
174 second(s)<o< 178 second(s)
(Round to the nearest whole number as needed.)
Two different waiting line configurations
Wait Times
Two Line (in seconds)
Single Line (in seconds)
64 215.7 85.7 339.8 200.1 63.9 157 142 278.9 252.9
630.2 333 328.8 915.3 553.1 475.9 477.9 474 401.9 722.3
596.9 865.2 1089.7 662.9 518.2 760.7 691.9 837.4 903.1 733.7
566.1 267.8 350.3 94.8 100.2 606.2 268.4 310 128.7 132.6
163.3 101.3 205.9 503.9 457 121.8 128.6 232.7 461.4 481.9
605.3 682.3 419.8 941.4 250.4 517.7 508.8 579.9 785.1 457
752.4 288.2 337 542.1 244 542.3 546.6 596.3 639.2 504.8
649.3 198.7 109.2 50.4 67.8 508 376.4 285.7 223.9 241
343.8 384.1 386.2 310 286.9 380.3 303.7 407.1 243.2 278.3
714.1 555.1 991.7 490.1 603.2 559.2 624.9 744.2 639 734.6
856.9 575 900 966.9 567.9 607.2 675.1 673.8 710.4 693.8
492.9 500.9 611 353.9 253.3 561.1 442.3 519.1 292.7 160.9
326.7 364.9 499.4 585.1 621.7 194.4 310.1 387.9 528.3 508.3
508.2 488.4 273 112.7 224.6 428.9 389.2 119.2 113 224.7
269.8 392.6 505.7 574.4 674.9 270.4 390.1 504.3 573.8 610.3
578.7 350.8 346.9 354.1 247 454.9 482.4 346.3 247
247 338.3
375.3 441.6 147.3 185.2 271.8 305.8 372.8 199.1 192.9 201.7
Print
Done
- X
Solution
Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman