The average annual return for a hedge fund in the United States in 2020 is considered to be normally distributed with μ = 13.5 percent and σ = 2.5 percent. (a) What is the probability that a hedge fund had an annual return of between 9.5 and 13 percent? Write out the solution in integral form and use the following R code to compute the numerical answer: pnorm(x2, mean = μ, sd = σ) − pnorm(x1, mean = μ, sd = σ) (b) What annual return would a hedge fund need to have in order to be in the top 10 percent of all hedge funds in the United States? Write out the equation we would need to solve in order to answer this question, then use the qnorm() function in R to find this score.
The average annual return for a hedge fund in the United States in 2020 is considered to be
(a) What is the
pnorm(x2,
(b) What annual return would a hedge fund need to have in order to be in the top 10 percent of all hedge funds in the United States? Write out the equation we would need to solve in order to answer this question, then use the qnorm()
Normal Distribution :
The normal distribution is defined by the following probability density function, where μ is the population mean and σ2 is the variance.
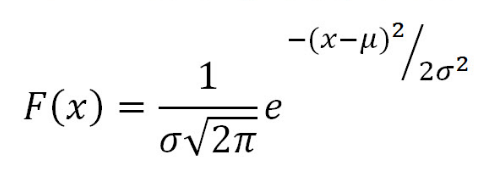
If a random variable X follows the normal distribution, then we write:
X ~ N (μ , σ)
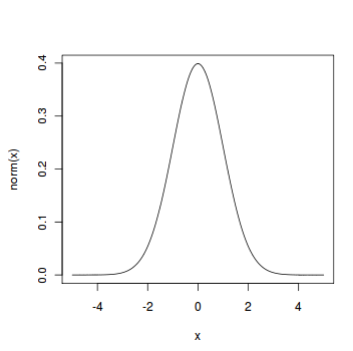
In particular, the normal distribution with μ = 0 and σ = 1 is called the standard normal distribution, and is denoted as N(0,1). It can be graphed as follows.
Step by step
Solved in 3 steps with 2 images









