The amount of calories consumed by customers at the Chinese buffet is normally distributed with mean 2762 and standard deviation 678. One randomly selected customer is observed to see how many calories X that customer consumes. Round all answers to 4 decimal places where possible. a. What is the distribution of X? X ~ N(,) b. Find the probability that the customer consumes less than 2519 calories. c. What proportion of the customers consume over 2910 calories? d. The Piggy award will given out to the 2% of customers who consume the most calories. What is the fewest number of calories a person must consume to receive the Piggy award? calories. (Round to the nearest calorie) Can you please answer all parts. I am not sure if possible, figured I'd ask.
The amount of calories consumed by customers at the Chinese buffet is
a. What is the distribution of X? X ~ N(,)
b. Find the
c. What proportion of the customers consume over 2910 calories?
d. The Piggy award will given out to the 2% of customers who consume the most calories. What is the fewest number of calories a person must consume to receive the Piggy award? calories. (Round to the nearest calorie)
Can you please answer all parts. I am not sure if possible, figured I'd ask.
Given Information :
The amount of calories consumed by customers at the Chinese buffet is normally distributed with mean 2762 and standard deviation 678. One randomly selected customer is observed to see how many calories X that customer consumes.
(a)
Define random variable X denotes amount of calories consumed by customers .
Here, X ~ N (μ=2762, σ=678)
(b)
We need to compute P. The corresponding z-value needed to be computed :
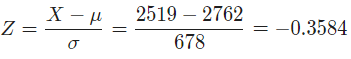
Therefore,
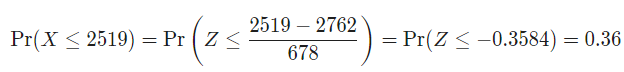
Probability that the customer consumes less than 2519 calories = 0.36 .
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 4 images









