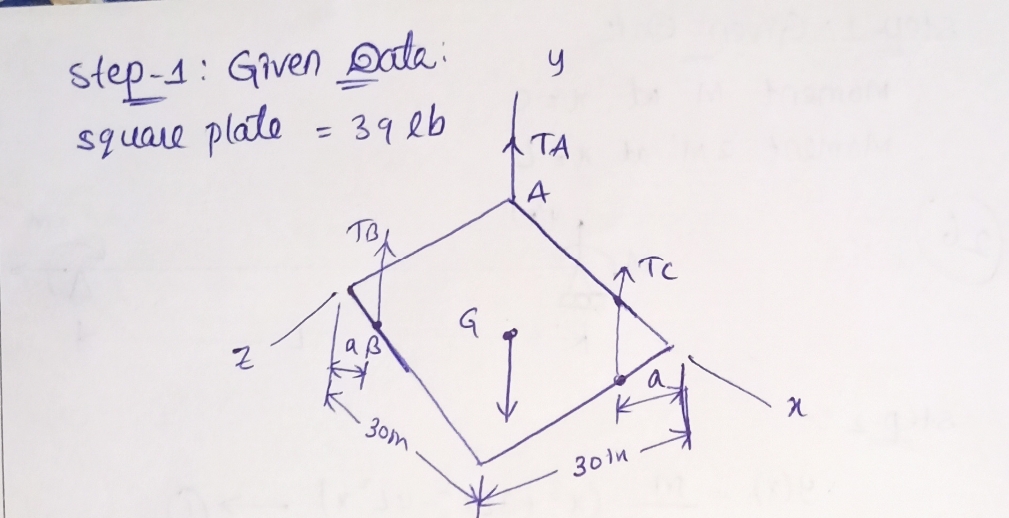
The 39-lb square plate shown is supported by three vertical wires. Determine the value of a for which the tension in each wire is equal. B 30 in. y Solution: . Construct the FBD A Jeanch 2. There are in total 30 in. 1. The weight of the plate should be added to the → forces and • Presenting all forces and couples using components: 1. Weight of the plate W = 2. Tension on A, TA = 3. Tension on B, TB = 4. Tension on C, Tc = i + i+ i+ i+ j+ + couples on the FB. j+ k (lb); k (lb); ◆ of the plate, lable this point as point G; k (lb); k (lb) is evenly distributed into three cables, hence:
The 39-lb square plate shown is supported by three vertical wires. Determine the value of a for which the tension in each wire is equal. B 30 in. y Solution: . Construct the FBD A Jeanch 2. There are in total 30 in. 1. The weight of the plate should be added to the → forces and • Presenting all forces and couples using components: 1. Weight of the plate W = 2. Tension on A, TA = 3. Tension on B, TB = 4. Tension on C, Tc = i + i+ i+ i+ j+ + couples on the FB. j+ k (lb); k (lb); ◆ of the plate, lable this point as point G; k (lb); k (lb) is evenly distributed into three cables, hence:
Chapter2: Loads On Structures
Section: Chapter Questions
Problem 1P
Related questions
Question
Hw #4
![**Problem Statement:**
The 39-lb square plate shown is supported by three vertical wires. Determine the value of \( a \) for which the tension in each wire is equal.
**Diagram Explanation:**
The diagram shows a square plate with three points labeled \( A \), \( B \), and \( C \). These points represent the attachment of the three supporting wires (not shown in the image) that hold the plate. The square plate has sides of 30 inches. The distances \( a \) marked on the diagram indicate that points \( B \) and \( C \) are symmetrically located along the sides of the plate.
**Solution:**
- **Construct the FBD (Free Body Diagram):**
1. The weight of the plate should be added to the __[blank]__ of the plate, label this point as point G.
2. There are in total __[blank]__ forces and __[blank]__ couples on the FBD.
- **Presenting all forces and couples using components:**
1. Weight of the plate \( W = (i + [\space] j + [\space] k) \) lb is evenly distributed into three cables, hence:
2. Tension on \( A, T_A = (i + [\space] j + [\space] k) \) lb;
3. Tension on \( B, T_B = (i + [\space] j + [\space] k) \) lb;
4. Tension on \( C, T_C = (i + [\space] j + [\space] k) \) lb.
**Note:** The blanks in the solution indicate areas where students need to fill in the appropriate values or concepts as part of the educational exercise.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9a42e238-4116-4e80-81a7-f4d567b4bd0e%2Fd7d232ff-b623-47c3-ba6b-0178ca150a3d%2Fqo0q0ks_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
The 39-lb square plate shown is supported by three vertical wires. Determine the value of \( a \) for which the tension in each wire is equal.
**Diagram Explanation:**
The diagram shows a square plate with three points labeled \( A \), \( B \), and \( C \). These points represent the attachment of the three supporting wires (not shown in the image) that hold the plate. The square plate has sides of 30 inches. The distances \( a \) marked on the diagram indicate that points \( B \) and \( C \) are symmetrically located along the sides of the plate.
**Solution:**
- **Construct the FBD (Free Body Diagram):**
1. The weight of the plate should be added to the __[blank]__ of the plate, label this point as point G.
2. There are in total __[blank]__ forces and __[blank]__ couples on the FBD.
- **Presenting all forces and couples using components:**
1. Weight of the plate \( W = (i + [\space] j + [\space] k) \) lb is evenly distributed into three cables, hence:
2. Tension on \( A, T_A = (i + [\space] j + [\space] k) \) lb;
3. Tension on \( B, T_B = (i + [\space] j + [\space] k) \) lb;
4. Tension on \( C, T_C = (i + [\space] j + [\space] k) \) lb.
**Note:** The blanks in the solution indicate areas where students need to fill in the appropriate values or concepts as part of the educational exercise.

Transcribed Image Text:Transcribing the content for an educational website:
---
### Presenting All Forces and Couples Using Components:
1. **Weight of the Plate \( W \) =**
\( \square \, i + \square \, j + \square \, k \) (lb) is evenly distributed into three cables, hence:
2. **Tension on \( A, \, T_A =**
\( \square \, i + \square \, j + \square \, k \) (lb);
3. **Tension on \( B, \, T_B =**
\( \square \, i + \square \, j + \square \, k \) (lb);
4. **Tension on \( C, \, T_C =**
\( \square \, i + \square \, j + \square \, k \) (lb);
### Taking the Moment About Point A:
1. **Position Vectors:**
- \( \vec{r}_{AB} = \square \, i + \square \, j + \square \, k \) (in);
- \( \vec{r}_{AC} = \square \, i + \square \, j + \square \, k \) (in);
- \( \vec{r}_{AG} = \square \, i + \square \, j + \square \, k \) (in);
2. **\( \Sigma M_A = 0 \):**
- \( M_A^{T_A} = \square \, i + \square \, j + \square \, k \) (lb-in);
- \( M_A^{T_B} = \square \, i + \square \, j + \square \, k \) (lb-in);
- \( M_A^{T_C} = \square \, i + \square \, j + \square \, k \) (lb-in);
- \( M_A^W = \square \, i + \square \, j + \square \, k \) (lb-in);
### Equilibrium Equations:
1. **\( \Sigma M_A = 0 \):** solve for \( a = \square \) in.
---
This transcription provides placeholders (⍰) for values to be filled in, allowing users to complete calculations
Expert Solution
Step 1
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you


Structural Analysis (10th Edition)
Civil Engineering
ISBN:
9780134610672
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning


Structural Analysis (10th Edition)
Civil Engineering
ISBN:
9780134610672
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning

Fundamentals of Structural Analysis
Civil Engineering
ISBN:
9780073398006
Author:
Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel Lanning
Publisher:
McGraw-Hill Education


Traffic and Highway Engineering
Civil Engineering
ISBN:
9781305156241
Author:
Garber, Nicholas J.
Publisher:
Cengage Learning