I need help with the explanation for how to find if True or False and why...For the first 3 statements I'm unsure how to check or understand why they are true or false but I believe the the following for them is 50 T, 51 T (If P false and Q false then True... don't understand why P is false in this case though...), 52 TFor Negations, Converse and Contrapositives how do I know if they are true or not? Is it if Original in True then Negation is False? If Original True Contrapositive True? What about Converse? **Question 50**: For all natural numbers \( a \), \( a^2 \equiv 0 \pmod{4} \) or \( a^2 \equiv 1 \pmod{4} \).**Question 51**: For all natural numbers \( a \), if \( a^2 \equiv 2 \pmod{4} \), then \( 1 = 2 \).**Question 52**: For all natural numbers \( a \), if \( a^2 \equiv 2 \pmod{4} \), then \( 1 \neq 2 \).**Question 53**: The negation of #51 is true.**Question 54**: The negation of #52 is true.**Question 55**: The converse of #51 is true.**Question 56**: The converse of #52 is true.**Question 57**: The contrapositive of #51 is true.**Question 58**: The contrapositive of #52 is true.**Question 59**: The contrapositive of #52 is true.

Answered: Image /qna-images/answer/9eb34133-4047-4a96-bc07-e5c443a29cfc.jpg

T T T T T T T T T T F 50. For all natural numbers a, a² = 0 (mod 4) or a² = 1(mod 4) F 51. For all natural numbers a, If a² = 2 (mod 4), then 1 = 2. For all natural numbers a, If a² = 2 (mod 4), then 1 ‡ 2. The negation #51 is true. The negation # 52 is true. F 52. F 53. F 54. F 55. The converse of #51 is true. F 56. The converse of #52 is true. F 57. The contrapositive of #51 is true. The contrapositive of #52 is true. F 58. Е 59 The contrapositive of #52 is true

T T T T T T T T T T F 50. For all natural numbers a, a² = 0 (mod 4) or a² = 1(mod 4) F 51. For all natural numbers a, If a² = 2 (mod 4), then 1 = 2. For all natural numbers a, If a² = 2 (mod 4), then 1 ‡ 2. The negation #51 is true. The negation # 52 is true. F 52. F 53. F 54. F 55. The converse of #51 is true. F 56. The converse of #52 is true. F 57. The contrapositive of #51 is true. The contrapositive of #52 is true. F 58. Е 59 The contrapositive of #52 is true

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

O 3. The conditional statement is "If I study, my grades will improve." What is the following statement in reference to the conditional statement? "If I do not study, then my grades will not improve." O converse contrapositive O inverse O conditional PREVIOUS 3 of 4 NEXT P Type here to search WE R S D F B N M
Answer 4-10
Which of the following is the algebraic form for the verbal statement shown? * "13 less than the product of 4 and a number, n, is 5" -- 13 = 5 4n – 13 = 5 4 O Option 1 O Option 2
An argument is expressed in English below. Catalina is sleepy or Catalina is not shocked. Catalina is excited. : Catalina is excited or Catalina is sleepy. Variable names are assigned to each English phrase as follows: •p: Catalina is excited •q: Catalina is shocked •r: Catalina is sleepy What is the form of the argument? Pick Pick v : Pick v
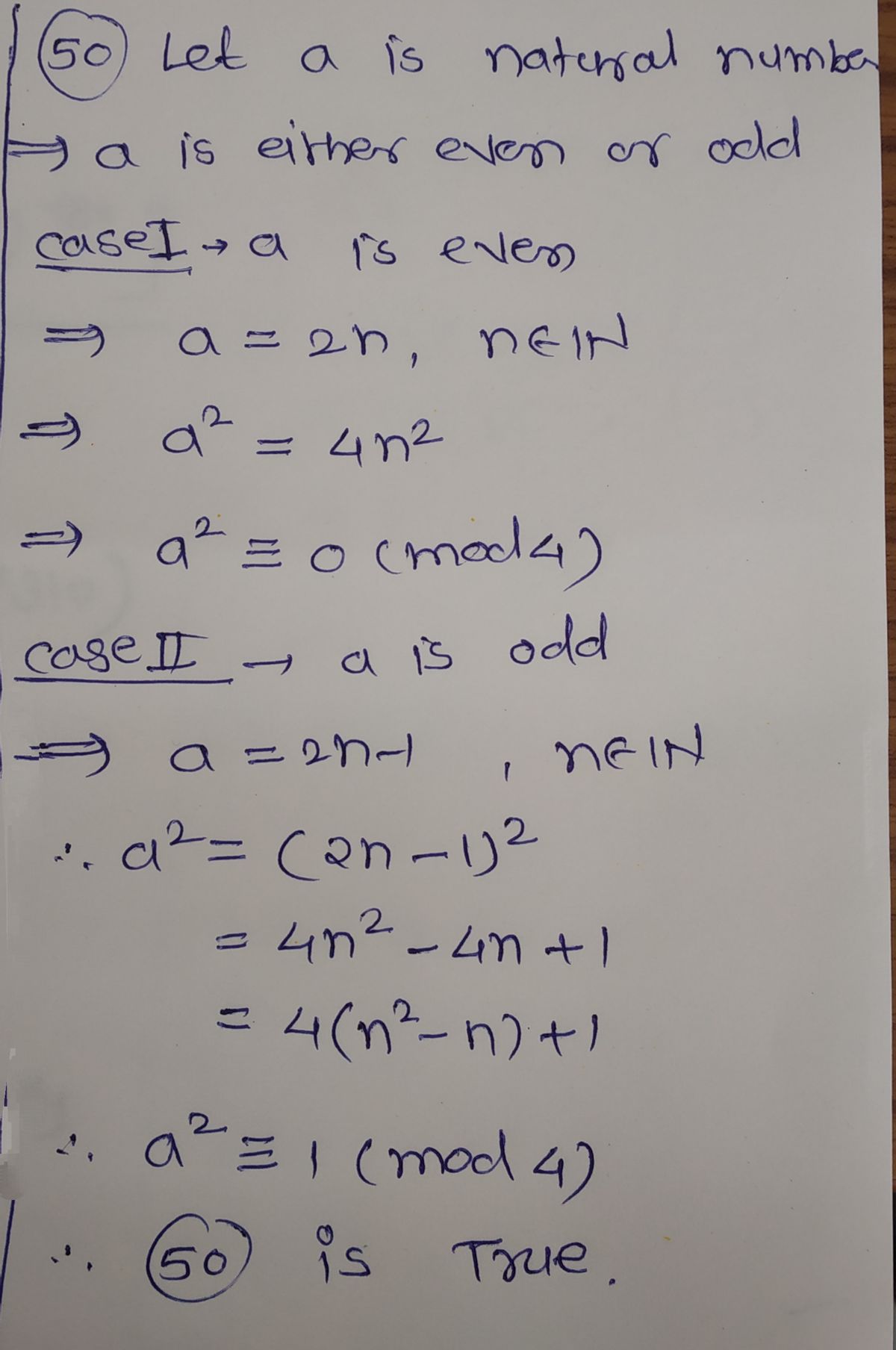
I didn’t understand how to solve these examples. Please help me understanding it step by step.