t S g Call the solution y₁ (t). b. Observe that the only difference between equations (31) and (32) is the constant -b in equation (31). Therefore, it may seem reasonable to assume that the solutions of these two equations also differ only by a constant. Test this assumption by trying to find a constant k such that y = yı(t) + k is a solution of equation (31). c. Compare your solution from part b with the solution given in the text in equation (17). Note: This method can also be used in some cases in which the constant b is replaced by a function g(t). It depends on whether you can guess the general form that the solution is likely to take. This method is described in detail in Section 3.5 in connection with second- order equations. 6. Use the method of Problem 5 to solve the equation 7. The field mouse differential equation dy -ay+b. dt population in Example 1 satisfies the = ODE dy P dt 2 - - - 450. a. Find the time at which the population becomes extinct if p(0) = 850. b. Find the time of extinction if p(0) = Po, where 0 < Po < 900. Nc. Find the initial population po if the population is to become extinct in 1 year. 8. The falling object in Example 2 satisfies the initial value
t S g Call the solution y₁ (t). b. Observe that the only difference between equations (31) and (32) is the constant -b in equation (31). Therefore, it may seem reasonable to assume that the solutions of these two equations also differ only by a constant. Test this assumption by trying to find a constant k such that y = yı(t) + k is a solution of equation (31). c. Compare your solution from part b with the solution given in the text in equation (17). Note: This method can also be used in some cases in which the constant b is replaced by a function g(t). It depends on whether you can guess the general form that the solution is likely to take. This method is described in detail in Section 3.5 in connection with second- order equations. 6. Use the method of Problem 5 to solve the equation 7. The field mouse differential equation dy -ay+b. dt population in Example 1 satisfies the = ODE dy P dt 2 - - - 450. a. Find the time at which the population becomes extinct if p(0) = 850. b. Find the time of extinction if p(0) = Po, where 0 < Po < 900. Nc. Find the initial population po if the population is to become extinct in 1 year. 8. The falling object in Example 2 satisfies the initial value
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
Related questions
Question
5 (a,b,c)
please

Transcribed Image Text:how the so
a. dy/dt = -y+5,
b. dy/dt = -2y +5,
c. dy/dt = -2y + 10,
2. Follow the instructions for Problem 1 for the following
initial-value problems:
G
y(0)
yo
y(0) = yo
a. dy/dt = y-5, y(0) = yo
G b. dy/dt = 2y-5,
c. dy/dt = 2y - 10, y(0) = yo
3. Consider the differential equation
dy/dt = -ay+b,
where both a and b are positive numbers.
a. Find the general solution of the differential equation.
G b. Sketch the solution for several different initial conditions.
c. Describe how the solutions change under each of the
following conditions:
i.
a increases.
y(0) = yo
y(0) = yo
ii.
b increases.
iii. Both a and b increase, but the ratio b/a remains the same.
4. Consider the differential equation dy/dt = ay - b.
a. Find the equilibrium solution ye.
b. Let Y(t) = y - ye; thus Y(t) is the deviation from the
equilibrium solution. Find the differential equation satisfied by
Y(t).
5. Undetermined Coefficients. Here is an alternative way to solve
the equation
lok sa
dy
dt
a. Solve the simpler equation
dy
dt
=ay - b.
= ay.
(31)
reason
also c
to fin
equat
C. C
the t
Note: Th
constant
can gues
method i
order eq
6. U:
(32)
7. T
differe
a
1
8.
prob

Transcribed Image Text:how the so
a. dy/dt = -y+5,
b. dy/dt = -2y +5,
c. dy/dt = -2y + 10,
2. Follow the instructions for Problem 1 for the following
initial-value problems:
G
y(0)
yo
y(0) = yo
a. dy/dt = y-5, y(0) = yo
G b. dy/dt = 2y-5,
c. dy/dt = 2y - 10, y(0) = yo
3. Consider the differential equation
dy/dt = -ay+b,
where both a and b are positive numbers.
a. Find the general solution of the differential equation.
G b. Sketch the solution for several different initial conditions.
c. Describe how the solutions change under each of the
following conditions:
i.
a increases.
y(0) = yo
y(0) = yo
ii.
b increases.
iii. Both a and b increase, but the ratio b/a remains the same.
4. Consider the differential equation dy/dt = ay - b.
a. Find the equilibrium solution ye.
b. Let Y(t) = y - ye; thus Y(t) is the deviation from the
equilibrium solution. Find the differential equation satisfied by
Y(t).
5. Undetermined Coefficients. Here is an alternative way to solve
the equation
lok sa
dy
dt
a. Solve the simpler equation
dy
dt
=ay - b.
= ay.
(31)
reason
also c
to fin
equat
C. C
the t
Note: Th
constant
can gues
method i
order eq
6. U:
(32)
7. T
differe
a
1
8.
prob
Expert Solution
Step 1
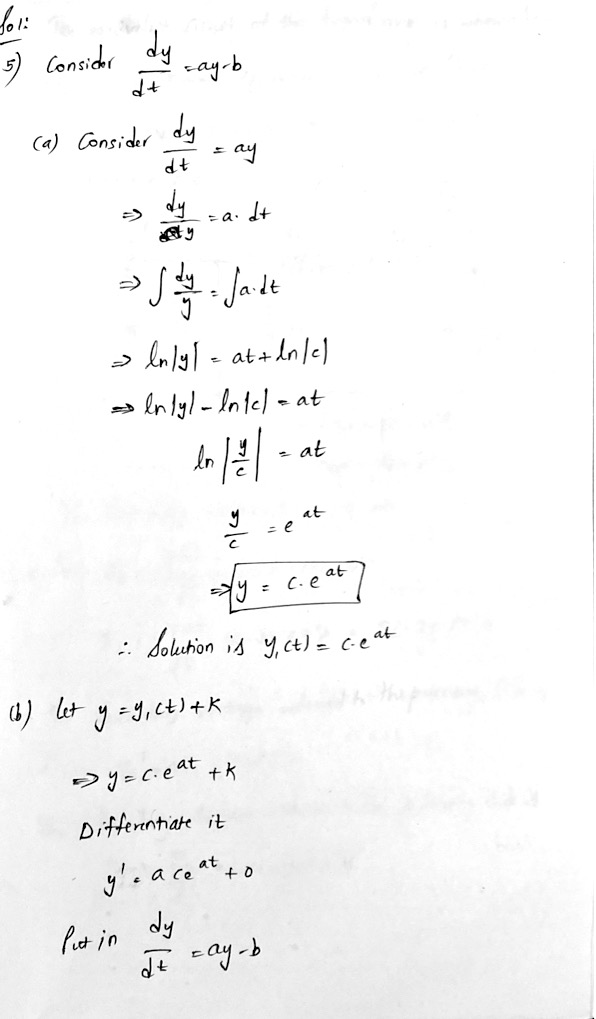
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education

Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON

Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,