S(x) = e¬z+5z-_1
Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
a) Determines the number of Zeropoints

The given function be f(x)=e^(-4x^(-4)+5x^(-2)-1)
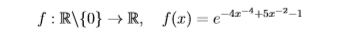
As it is a exponential function , it is better to solve by using graphing calculator, As in the power of 'e' there are function of negative power of 'x ', so we take a deleted neighbourhood of '0'. In graph below we can see that for taking small radius r=0.265 and we can see tha |x-0|<r there we gate infinite number of zeros of the given function. , So any small (<r) deleted neighbourhood of zero we get infinite zeros of this fuction

Step by step
Solved in 4 steps with 3 images









