Suppose you get for free one of the following two securities: (a) an annuity that pays $10,000 at the end of each of the next 10 years. (b) a perpetuity that pays $10,000 forever, but skips the first 10 payments, meaning the first cash payment from this security is 11 years from today. Which security would you choose if the annual interest rate at all maturities is 4%? Does your answer change if the interest rate at all maturities is 7.5%? Why or why not?
3. Suppose you get for free one of the following two securities:
(a) an
(b) a perpetuity that pays $10,000 forever, but skips the first 10 payments, meaning
the first cash payment from this security is 11 years from today.
Which security would you choose if the annual interest rate at all maturities is 4%?
Does your answer change if the interest rate at all maturities is 7.5%? Why or why
not?
The choice between the two securities depends on the interest rate. The present value of an annuity can be calculated as the sum of the present value of each future payment, and the present value of a perpetuity can be calculated as the future payment divided by the discount rate.
The present value of an annuity is the current worth of a series of future payments, taking into account the time value of money and a discount rate. The time value of money reflects the idea that a dollar received today is worth more than a dollar received in the future, because the dollar received today can be invested and earn a return. The discount rate is used to reflect the opportunity cost of holding the annuity instead of investing the money in a different security.
The formula for calculating the present value of an annuity is:
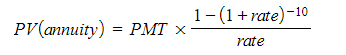
where: PMT is the amount of each payment,
r is the discount rate,
n is the number of payments.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images









