Suppose the function y = h(x) is nonnegative and continuous on (a.B), which implies that the area bounded by the graph of h and the x-axis on [a.p] equals h(x) dx or ay dx. If the graph of y=h(x) on [a,b] is traced exactly once by the parametric equations x = f(t), y = g(t), for a st≤ b, then it follows by substitution that the area bounded by h is given by the equation below. [ n(x) dx = Sy dx = g(t) f(t) dt, if a = f(a) and ß= f(b) (or Find the area of the region bounded by the astroid x = 9 cos ³t, y=9 sin ³t, for 0 st≤ 2. Click the icon to view an example of an astroid graph. h(x) dx = g(1) f(t) dt, if a = f(b) and p = f(a)) The area is (Type an exact answer, using x as needed.)
Suppose the function y = h(x) is nonnegative and continuous on (a.B), which implies that the area bounded by the graph of h and the x-axis on [a.p] equals h(x) dx or ay dx. If the graph of y=h(x) on [a,b] is traced exactly once by the parametric equations x = f(t), y = g(t), for a st≤ b, then it follows by substitution that the area bounded by h is given by the equation below. [ n(x) dx = Sy dx = g(t) f(t) dt, if a = f(a) and ß= f(b) (or Find the area of the region bounded by the astroid x = 9 cos ³t, y=9 sin ³t, for 0 st≤ 2. Click the icon to view an example of an astroid graph. h(x) dx = g(1) f(t) dt, if a = f(b) and p = f(a)) The area is (Type an exact answer, using x as needed.)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![Suppose the function \( y = h(x) \) is nonnegative and continuous on \([ \alpha, \beta ]\), which implies that the area bounded by the graph of \( h \) and the x-axis on \([ \alpha, \beta ]\) equals \(\int_{\alpha}^{\beta} h(x) \, dx\) or \(\int_{\alpha}^{\beta} y \, dx\). If the graph of \( y = h(x) \) on \([ \alpha, \beta ]\) is traced exactly once by the parametric equations \( x = f(t) \), \( y = g(t) \), for \( a \le t \le b \), then it follows by substitution that the area bounded by \( h \) is given by the equation below:
\[
\int_{\alpha}^{\beta} h(x) \, dx = \int_{a}^{b} y \, dx = \int_{a}^{b} g(t) f'(t) \, dt, \text{ if } \alpha = f(a) \text{ and } \beta = f(b)
\]
or
\[
\int_{\alpha}^{\beta} h(x) \, dx = \int_{a}^{b} g(t) f'(t) \, dt, \text{ if } \alpha = f(b) \text{ and } \beta = f(a)
\]
Find the area of the region bounded by the astroid: \( x = 9 \cos^3 t \), \( y = 9 \sin^3 t \), for \( 0 \le t \le 2\pi \).
**Note**: Click the icon to view an example of an astroid graph.
---
The area is \(\square\).
(Type an exact answer, using \(\pi\) as needed.)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F14ca10a7-9a5a-4024-afbf-f0f142f43830%2F084b9c7b-20bd-4342-821c-c3fb5dce4fde%2Fgccv9g_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Suppose the function \( y = h(x) \) is nonnegative and continuous on \([ \alpha, \beta ]\), which implies that the area bounded by the graph of \( h \) and the x-axis on \([ \alpha, \beta ]\) equals \(\int_{\alpha}^{\beta} h(x) \, dx\) or \(\int_{\alpha}^{\beta} y \, dx\). If the graph of \( y = h(x) \) on \([ \alpha, \beta ]\) is traced exactly once by the parametric equations \( x = f(t) \), \( y = g(t) \), for \( a \le t \le b \), then it follows by substitution that the area bounded by \( h \) is given by the equation below:
\[
\int_{\alpha}^{\beta} h(x) \, dx = \int_{a}^{b} y \, dx = \int_{a}^{b} g(t) f'(t) \, dt, \text{ if } \alpha = f(a) \text{ and } \beta = f(b)
\]
or
\[
\int_{\alpha}^{\beta} h(x) \, dx = \int_{a}^{b} g(t) f'(t) \, dt, \text{ if } \alpha = f(b) \text{ and } \beta = f(a)
\]
Find the area of the region bounded by the astroid: \( x = 9 \cos^3 t \), \( y = 9 \sin^3 t \), for \( 0 \le t \le 2\pi \).
**Note**: Click the icon to view an example of an astroid graph.
---
The area is \(\square\).
(Type an exact answer, using \(\pi\) as needed.)
Expert Solution
Step 1: To find
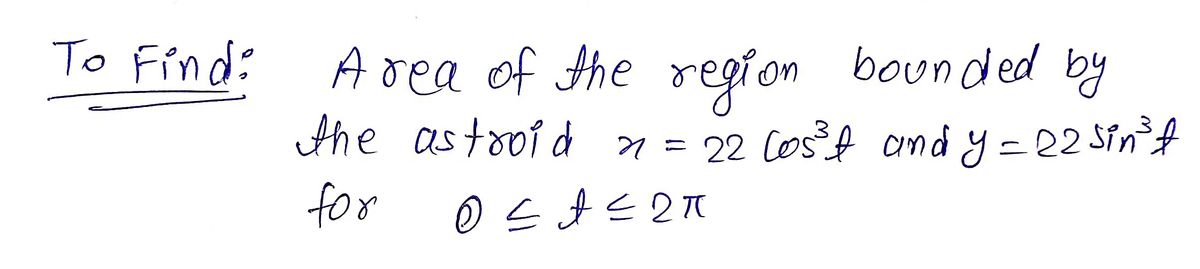
Step by step
Solved in 3 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

