Suppose that the sequence x0, x₁, x2... is defined by xo = 3, x₁ = 6, and xk+2=-6xk+1-5xk for k20. Find a general formula for x. Be sure to include parentheses where necessary, e.g. to distinguish 1/(2k) from 1/2k.
Suppose that the sequence x0, x₁, x2... is defined by xo = 3, x₁ = 6, and xk+2=-6xk+1-5xk for k20. Find a general formula for x. Be sure to include parentheses where necessary, e.g. to distinguish 1/(2k) from 1/2k.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![Suppose that the sequence \( x_0, x_1, x_2, \ldots \) is defined by \( x_0 = 3 \), \( x_1 = 6 \), and \( x_{k+2} = -6x_{k+1} - 5x_k \) for \( k \geq 0 \). Find a general formula for \( x_k \). Be sure to include parentheses where necessary, e.g., to distinguish \( 1/(2k) \) from \( 1/2k \).
\[ x_k = 0 \]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F564c5eb4-4e12-4a6c-879a-b39210fe38a5%2F93c7f833-0d45-4992-98e4-0517d7c84891%2Fzvhn9ob_processed.png&w=3840&q=75)
Transcribed Image Text:Suppose that the sequence \( x_0, x_1, x_2, \ldots \) is defined by \( x_0 = 3 \), \( x_1 = 6 \), and \( x_{k+2} = -6x_{k+1} - 5x_k \) for \( k \geq 0 \). Find a general formula for \( x_k \). Be sure to include parentheses where necessary, e.g., to distinguish \( 1/(2k) \) from \( 1/2k \).
\[ x_k = 0 \]
Expert Solution
Step 1
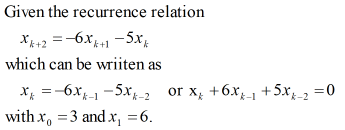
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

