Suppose that p, q,r and s are propositions. Determine if the following argument is valid using any appropriate means. Support your answer. (p → q) (r → s) (p V r) → (q V s)
Suppose that p, q,r and s are propositions. Determine if the following argument is valid using any appropriate means. Support your answer. (p → q) (r → s) (p V r) → (q V s)
Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
Chapter1: Line And Angle Relationships
Section1.5: The Format Proof Of A Theorem
Problem 11E: When can a theorem be cited as a reason reason in a proof?
Related questions
Topic Video
Question
This is a discrete math question. This could be solved using truth table. I am just confused. I really need help to do solve this problem.

Transcribed Image Text:### Logical Properties and Statements
**Logical Equivalences:**
- **Idempotence:**
- \( p \lor p \equiv p \)
- \( p \land p \equiv p \)
- **Commutativity:**
- \( p \lor q \equiv q \lor p \)
- \( p \land q \equiv q \land p \)
- **Associativity:**
- \( p \lor (q \lor r) \equiv (p \lor q) \lor r \)
- \( p \land (q \land r) \equiv (p \land q) \land r \)
- **Distributivity:**
- \( p \lor (q \land r) \equiv (p \lor q) \land (p \lor r) \)
- \( p \land (q \lor r) \equiv (p \land q) \lor (p \land r) \)
- **Absorptivity:**
- \( p \lor (p \land q) \equiv p \)
- \( p \land (p \lor q) \equiv p \)
- **Identity:**
- \( p \lor \bot \equiv p \)
- \( p \land \top \equiv p \)
- **Complementarity:**
- \( p \lor (\neg p) \equiv \top \)
- \( p \land (\neg p) \equiv \bot \)
- **Dominance:**
- \( p \lor \top \equiv \top \)
- \( p \land \bot \equiv \bot \)
- **Involution:**
- \( \neg (\neg p) \equiv p \)
- **Exclusivity:**
- \( \neg (\top) \equiv \bot \)
- \( \neg (\bot) \equiv \top \)
- **DeMorgan’s:**
- \( \neg (p \lor q) \equiv (\neg p) \land (\neg q) \)
- \( \neg (p \land q) \equiv (\neg p) \lor (\neg q) \)
### Logical Inferences
- **Adjunction:**
- \( \frac{p
![Suppose that \( p, q, r \) and \( s \) are propositions. Determine if the following argument is valid using any appropriate means. Support your answer.
\[
\begin{align*}
(p \rightarrow q) \quad (r \rightarrow s) \\
\hline
(p \lor r) \rightarrow (q \lor s)
\end{align*}
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3b34fbf0-f4e4-4f82-bff3-9489c249d683%2F1b4e1d93-93e2-4e3f-bdc2-8e16bae56b49%2F6jglwui_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Suppose that \( p, q, r \) and \( s \) are propositions. Determine if the following argument is valid using any appropriate means. Support your answer.
\[
\begin{align*}
(p \rightarrow q) \quad (r \rightarrow s) \\
\hline
(p \lor r) \rightarrow (q \lor s)
\end{align*}
\]
Expert Solution
Step 1
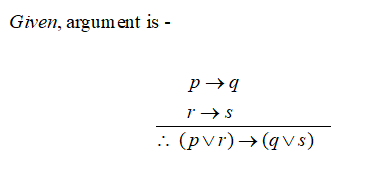

Step by step
Solved in 2 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,