Suppose that f(x, y) : = Y 1 + x at which {(x, y) | 0 ≤ x ≤ 1, - x≤ y ≤ √x}. a Then the double integral of f(x, y) over D is = [ f(x, y)dady Round your answer to four decimal places.
Suppose that f(x, y) : = Y 1 + x at which {(x, y) | 0 ≤ x ≤ 1, - x≤ y ≤ √x}. a Then the double integral of f(x, y) over D is = [ f(x, y)dady Round your answer to four decimal places.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
5.2.4
![**Mathematical Problem: Evaluating a Double Integral**
Let \( f(x, y) = \frac{y}{1+x} \) over the region \( D \), where:
\[ D = \{ (x, y) \mid 0 \leq x \leq 1, -x \leq y \leq \sqrt{x} \} \]
The graph depicts the region \( D \) on the Cartesian plane:
- It is bounded on the left by the vertical line at \( x = 0 \).
- The right boundary is the vertical line at \( x = 1 \).
- The lower boundary is the line \( y = -x \).
- The upper boundary is the curve \( y = \sqrt{x} \).
The region \( D \) appears as a triangular area with a curved hypotenuse, forming a combination of linear and parabolic boundaries.
**Objective:**
Calculate the double integral of \( f(x, y) \) over the region \( D \):
\[
\iint_D f(x, y) \, dx \, dy = \text{(Result rounded to four decimal places)}
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F876c9bbd-0074-4123-babe-119feafc9f73%2Ffd3ce499-dda5-4e39-8825-2e28cc38252c%2Feevt469_processed.png&w=3840&q=75)
Transcribed Image Text:**Mathematical Problem: Evaluating a Double Integral**
Let \( f(x, y) = \frac{y}{1+x} \) over the region \( D \), where:
\[ D = \{ (x, y) \mid 0 \leq x \leq 1, -x \leq y \leq \sqrt{x} \} \]
The graph depicts the region \( D \) on the Cartesian plane:
- It is bounded on the left by the vertical line at \( x = 0 \).
- The right boundary is the vertical line at \( x = 1 \).
- The lower boundary is the line \( y = -x \).
- The upper boundary is the curve \( y = \sqrt{x} \).
The region \( D \) appears as a triangular area with a curved hypotenuse, forming a combination of linear and parabolic boundaries.
**Objective:**
Calculate the double integral of \( f(x, y) \) over the region \( D \):
\[
\iint_D f(x, y) \, dx \, dy = \text{(Result rounded to four decimal places)}
\]
Expert Solution
Step 1
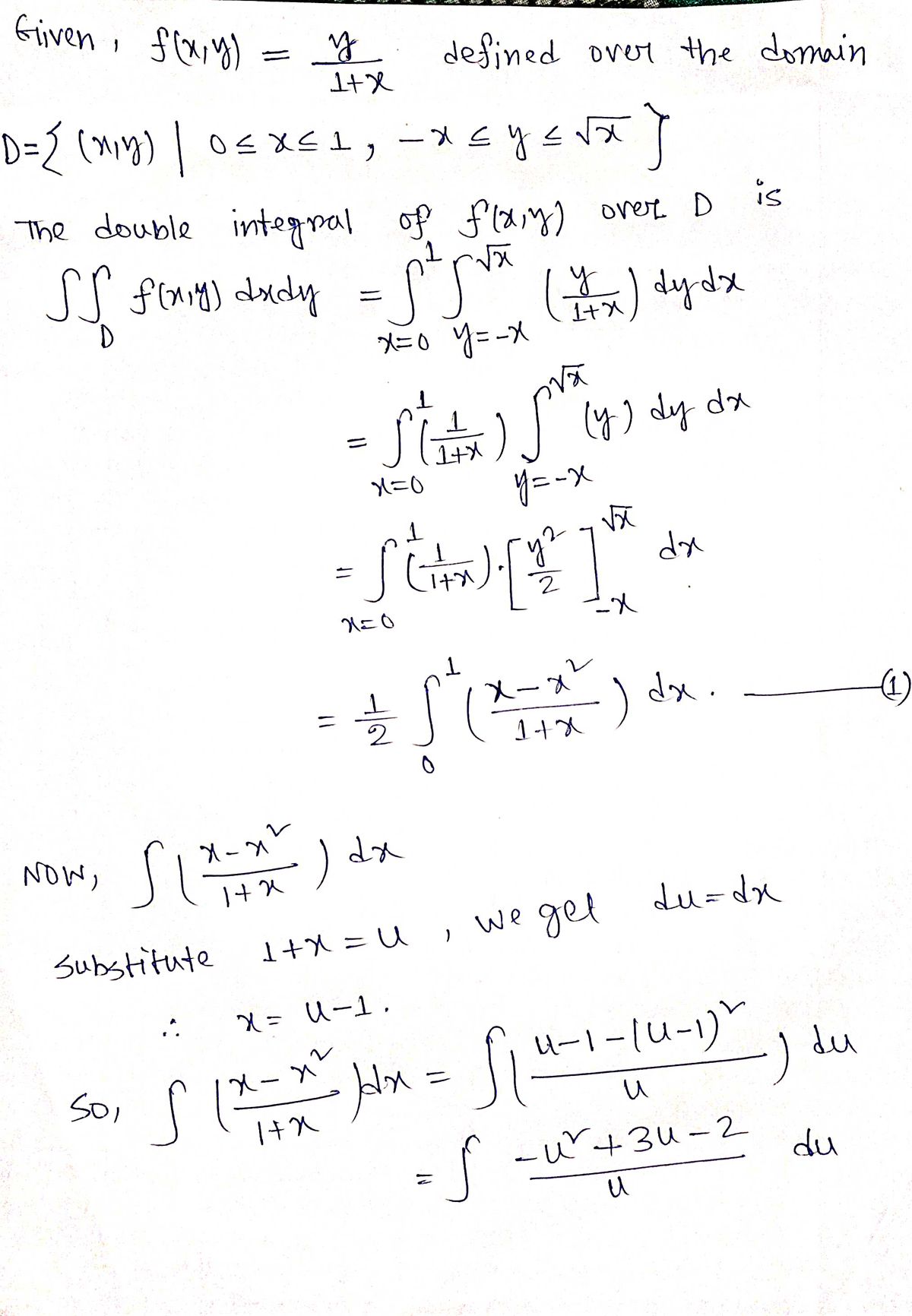
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

