Suppose that b₁ D₂ Dzi is a sequence defined as follows. bk = 5b ³|k/21] b₁ = 0 and b₂ = 3 True or False? For every integer n ≥ 1, b is divisible by 3. To answer this question, define a property P(n) as follows. P(n) is the sentence: "b, is divisible by 3." Is P(1) true? Is P(2) true? So, by definition of If P(i) is true for each integer i from 1 through k, is P(k + 1) true? Suppose k is any integer with kz 2 such that b, is divisible by 3 for each integer i with 1 sisk. Must it be true that Dk+1 Consider two cases: k is odd, and k is even. Case 1, k is odd: In this case k + 1 is Select- V and -Select- -=[ + ¹] - [ So, By k+1 is -Select- Case 2, k is even: In this case k + 1 is odd, and k+1=1 / + -Select- + 6 for every integer k 2 3 DI(+1)/21 = 5. --Select-- Therefore, Dk+1 It follows from cases (1) and (2) that either Now Dk+1= 5-D|(x+1)/2₁ +6 By -Select- = 0 and 0 is divisible by 3. So P(1) is true. is divisible by 3? = 3 and 3 is divisible by 3. So P(2) is true. Select V and, hence, +6 (Equation 1). by definition of b₁ D₂ D₂- by substitution from Equation 1 an integer. by factoring out a common factor. where k+1 - | ₁ + ² | = _*+₁ or | K + ¹] - [ b, is divisible by 3 for each integer / with 1 ≤ i ≤ k. So b|(k+1)/2) is divisible by -Select- V an integer. by definition of floor. divisible by 3 by -Select-- , this reasoning shows that b is divisible by 3 for , and, hence, in both cases, 1 s and so P(x + 1) is -Select- Select [K++|s , and, thus, by -Select- V sk. So the answer to the question is -Select- there is an integer r such th
Suppose that b₁ D₂ Dzi is a sequence defined as follows. bk = 5b ³|k/21] b₁ = 0 and b₂ = 3 True or False? For every integer n ≥ 1, b is divisible by 3. To answer this question, define a property P(n) as follows. P(n) is the sentence: "b, is divisible by 3." Is P(1) true? Is P(2) true? So, by definition of If P(i) is true for each integer i from 1 through k, is P(k + 1) true? Suppose k is any integer with kz 2 such that b, is divisible by 3 for each integer i with 1 sisk. Must it be true that Dk+1 Consider two cases: k is odd, and k is even. Case 1, k is odd: In this case k + 1 is Select- V and -Select- -=[ + ¹] - [ So, By k+1 is -Select- Case 2, k is even: In this case k + 1 is odd, and k+1=1 / + -Select- + 6 for every integer k 2 3 DI(+1)/21 = 5. --Select-- Therefore, Dk+1 It follows from cases (1) and (2) that either Now Dk+1= 5-D|(x+1)/2₁ +6 By -Select- = 0 and 0 is divisible by 3. So P(1) is true. is divisible by 3? = 3 and 3 is divisible by 3. So P(2) is true. Select V and, hence, +6 (Equation 1). by definition of b₁ D₂ D₂- by substitution from Equation 1 an integer. by factoring out a common factor. where k+1 - | ₁ + ² | = _*+₁ or | K + ¹] - [ b, is divisible by 3 for each integer / with 1 ≤ i ≤ k. So b|(k+1)/2) is divisible by -Select- V an integer. by definition of floor. divisible by 3 by -Select-- , this reasoning shows that b is divisible by 3 for , and, hence, in both cases, 1 s and so P(x + 1) is -Select- Select [K++|s , and, thus, by -Select- V sk. So the answer to the question is -Select- there is an integer r such th
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Title: Mathematical Induction Proof for Divisibility by 3**
**Description:**
The following is a step-by-step proof using mathematical induction to show that for every integer \( n \geq 1 \), the term \( b_n \) in the sequence is divisible by 3. The sequence is defined by:
- \( b_k = 5b_{\lfloor k/2 \rfloor} + 6 \) for every integer \( k \geq 3 \)
- \( b_1 = 0 \) and \( b_2 = 3 \)
**Proof Structure:**
1. **Define the Property \( P(n) \):**
\( P(n) \) is the statement: "The term \( b_n \) is divisible by 3."
2. **Base Cases:**
- **\( P(1) \) True?**
\( b_1 = 0 \) and 0 is divisible by 3. So \( P(1) \) is true.
- **\( P(2) \) True?**
\( b_2 = 3 \) and 3 is divisible by 3. So \( P(2) \) is true.
3. **Inductive Step:**
- Suppose \( k \) is any integer with \( k \geq 2 \) such that \( b_j \) is divisible by 3 for each integer \( j \) with \( 1 \leq j \leq k \).
- Must prove that \( b_{k+1} \) is divisible by 3.
4. **Consider Two Cases:**
- **Case 1, \( k \) is odd:**
In this scenario, \( k + 1 \) is even, and \( \left\lfloor \frac{k+1}{2} \right\rfloor = \frac{k+1}{2} \).
- **Case 2, \( k \) is even:**
Here, \( k + 1 \) is odd, and \( \left\lfloor \frac{k+1}{2} \right\rfloor = \frac{k}{2} \).
5. **Deriving a Common Conclusion:**
- From both cases (1) and (2), either \( \left\lf
Expert Solution
Step 1: Proof of the problem.
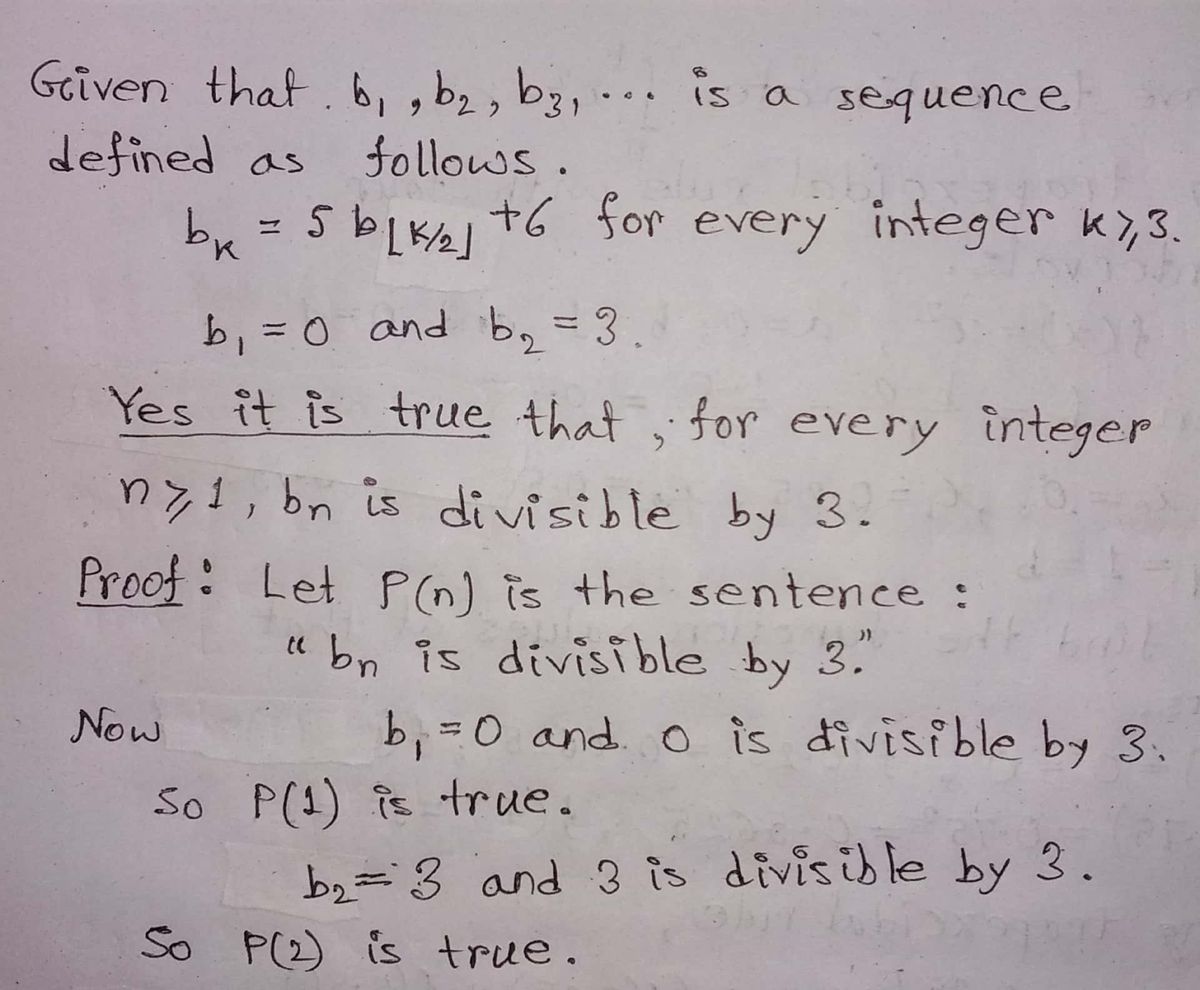
Step by step
Solved in 3 steps with 7 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

