Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Suppose that {a} and {b} are two sequences of real numbers where n = 1 to ∞, L and b L, where LER (i.e. L = +00). and that a n 72 2 Use the - N definition of limit to show that lima = L² n-∞ Definition of limit If XR, a is a limit point of X, and f: X → R, say that the limit of f on X at a is the number L provided that for every € > 0 there is a 8 >0 such that f (x) - L|< < whenever x EX and 0 < |ax| < 8.

Suppose that {a} and {b} are two sequences of real numbers where n = 1 to ∞, L and b L, where LER (i.e. L = +00). and that a n 72 2 Use the - N definition of limit to show that lima = L² n-∞ Definition of limit If XR, a is a limit point of X, and f: X → R, say that the limit of f on X at a is the number L provided that for every € > 0 there is a 8 >0 such that f (x) - L|< < whenever x EX and 0 < |ax| < 8.

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
Suppose that \(\{a_n\}\) and \(\{b_n\}\) are two sequences of real numbers where \(n = 1\) to \(\infty\), and that \(a_n \to L\) and \(b_n \to L\), where \(L \in \mathbb{R}\) (i.e., \(L \neq \pm\infty\)). Use the \(\varepsilon - N\) definition of limit to show that \(\lim_{n \to \infty} a_n^2 = L^2\). **Definition of limit** If \(X \subseteq \mathbb{R}\), \(a\) is a limit point of \(X\), and \(f: X \to \mathbb{R}\), say that the limit of \(f\) on \(X\) at \(a\) is the number \(L\) provided that for every \(\varepsilon > 0\) there is a \(\delta > 0\) such that \(|f(x) - L| < \varepsilon\) whenever \(x \in X\) and \(0 < |a - x| < \delta\).
Transcribed Image Text:Suppose that \(\{a_n\}\) and \(\{b_n\}\) are two sequences of real numbers where \(n = 1\) to \(\infty\), and that \(a_n \to L\) and \(b_n \to L\), where \(L \in \mathbb{R}\) (i.e., \(L \neq \pm\infty\)). Use the \(\varepsilon - N\) definition of limit to show that \(\lim_{n \to \infty} a_n^2 = L^2\). **Definition of limit** If \(X \subseteq \mathbb{R}\), \(a\) is a limit point of \(X\), and \(f: X \to \mathbb{R}\), say that the limit of \(f\) on \(X\) at \(a\) is the number \(L\) provided that for every \(\varepsilon > 0\) there is a \(\delta > 0\) such that \(|f(x) - L| < \varepsilon\) whenever \(x \in X\) and \(0 < |a - x| < \delta\).
Expert Solution
Step 1: Introduction

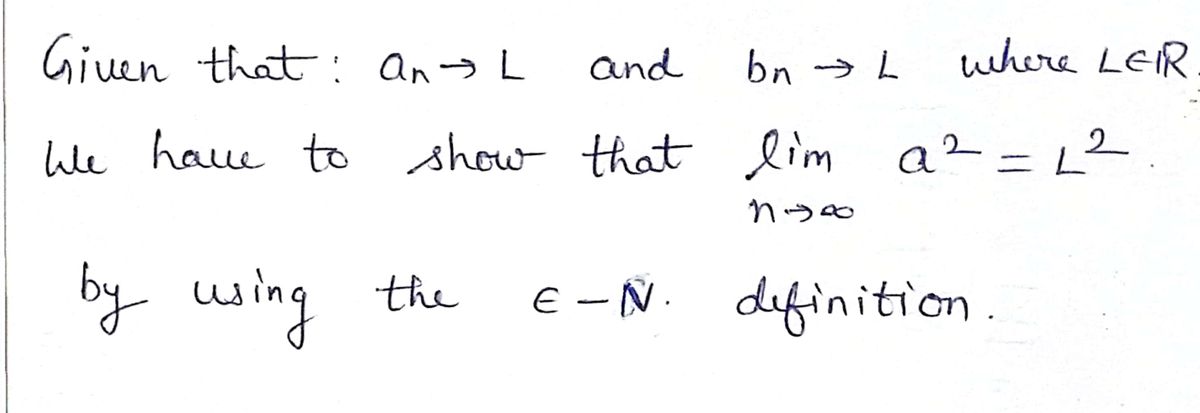
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS