Suppose p(x, y) = = 2x+y -₂x = 1, 2, 3, y = 1, 2 is the joint pmf of X and Y. Determine P (Y= 1). 33
Suppose p(x, y) = = 2x+y -₂x = 1, 2, 3, y = 1, 2 is the joint pmf of X and Y. Determine P (Y= 1). 33
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
please solve.
![Suppose \( p(x, y) = \frac{2x + y}{33} \), where \( x = 1, 2, 3 \) and \( y = 1, 2 \) is the joint pmf of \( X \) and \( Y \). Determine \( P(Y = 1) \).
### Explanation:
**Problem Context:**
- We are given a joint probability mass function (pmf) for two discrete random variables \( X \) and \( Y \).
- The function is defined as \( p(x, y) = \frac{2x + y}{33} \).
- The goal is to find the marginal probability \( P(Y = 1) \), which involves summing over all possible values of \( X \) while keeping \( Y \) fixed at 1.
**Steps to Solve:**
1. **Identify Domains:**
- \( x \) can take values from the set \{1, 2, 3\}.
- \( y \) takes values from the set \{1, 2\}.
2. **Marginal Probability \( P(Y = 1) \):**
- To find \( P(Y = 1) \), sum \( p(x, y) \) over all values of \( x \) for \( y = 1 \).
- Compute:
\[
P(Y = 1) = \sum_{x=1}^{3} p(x, 1) = p(1,1) + p(2,1) + p(3,1)
\]
3. **Calculate Each Component:**
- \( p(1,1) = \frac{2(1) + 1}{33} = \frac{3}{33} \)
- \( p(2,1) = \frac{2(2) + 1}{33} = \frac{5}{33} \)
- \( p(3,1) = \frac{2(3) + 1}{33} = \frac{7}{33} \)
4. **Sum and Simplify:**
- \( P(Y = 1) = \frac{3}{33} + \frac{5}{33} + \frac{7}{33} = \frac{15}{33} = \frac{5](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff5a46a21-656d-42a0-a455-81d241d5836d%2F3d2c6eb3-aba0-4ff9-a343-8b55f8b83746%2F4pidfwp_processed.png&w=3840&q=75)
Transcribed Image Text:Suppose \( p(x, y) = \frac{2x + y}{33} \), where \( x = 1, 2, 3 \) and \( y = 1, 2 \) is the joint pmf of \( X \) and \( Y \). Determine \( P(Y = 1) \).
### Explanation:
**Problem Context:**
- We are given a joint probability mass function (pmf) for two discrete random variables \( X \) and \( Y \).
- The function is defined as \( p(x, y) = \frac{2x + y}{33} \).
- The goal is to find the marginal probability \( P(Y = 1) \), which involves summing over all possible values of \( X \) while keeping \( Y \) fixed at 1.
**Steps to Solve:**
1. **Identify Domains:**
- \( x \) can take values from the set \{1, 2, 3\}.
- \( y \) takes values from the set \{1, 2\}.
2. **Marginal Probability \( P(Y = 1) \):**
- To find \( P(Y = 1) \), sum \( p(x, y) \) over all values of \( x \) for \( y = 1 \).
- Compute:
\[
P(Y = 1) = \sum_{x=1}^{3} p(x, 1) = p(1,1) + p(2,1) + p(3,1)
\]
3. **Calculate Each Component:**
- \( p(1,1) = \frac{2(1) + 1}{33} = \frac{3}{33} \)
- \( p(2,1) = \frac{2(2) + 1}{33} = \frac{5}{33} \)
- \( p(3,1) = \frac{2(3) + 1}{33} = \frac{7}{33} \)
4. **Sum and Simplify:**
- \( P(Y = 1) = \frac{3}{33} + \frac{5}{33} + \frac{7}{33} = \frac{15}{33} = \frac{5
Expert Solution
Step 1
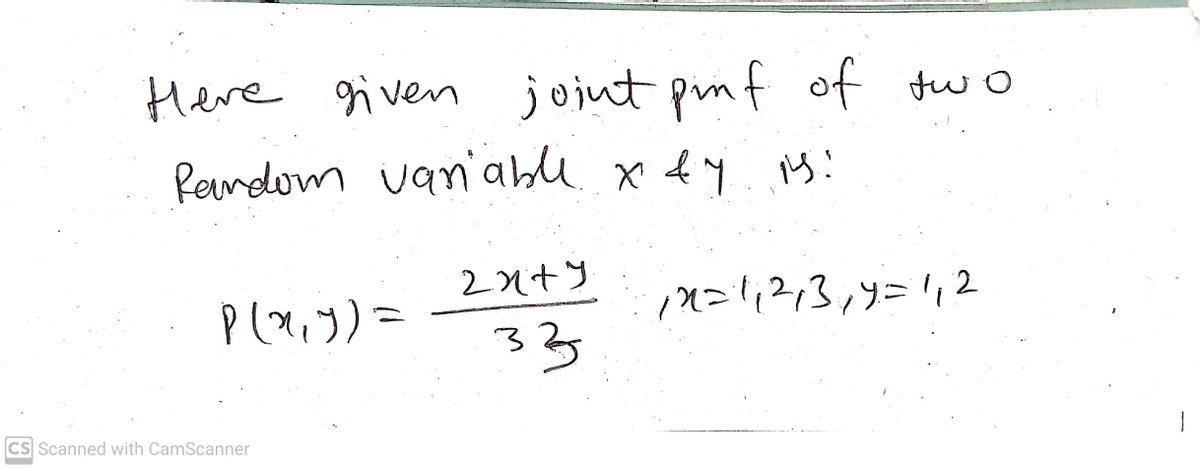
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman