Sulfur compounds cause “off-odors” in wine, so winemakers want to know the odor threshold, the lowest concentration of a compound that the human nose can detect. The odor threshold for dimethyl sulfide (DMS) in trained wine tasters is about 25 micrograms per liter of wine (μg/l). The untrained noses of consumers may be less sensitive, however. Here are the DMS odor thresholds for 10 untrained students: 31 31 43 36 23 34 32 30 20 24
Sulfur compounds cause “off-odors” in wine, so winemakers want to know the odor threshold, the lowest concentration of a compound that the human nose can detect. The odor threshold for dimethyl sulfide (DMS) in trained wine tasters is about 25 micrograms per liter of wine (μg/l). The untrained noses of consumers may be less sensitive, however. Here are the DMS odor thresholds for 10 untrained students:
31 31 43 36 23 34 32 30 20 24
Assume that the standard deviation of the odor threshold for untrained noses is known to be σ = 7 μg/l. The first condition of inference requires the 10 untrained students represent a simple random sample from all untrained consumers. This is not likely but we choose to believe so. The second condition requires the distribution of the thresholds for untrained noses is not too far from a normal distribution. Given the following stem plot, the second condition is also satisified.
2|034
3|011246
4|3
Give a 95% confidence interval for the mean DMS odor threshold among all students.
Is there evidence that the mean threshold for untrained tasters is greater than 25 μg/l? State the hypotheses.
Answer
For 95% confidence level, critical value iof z is 1.96 .
The required sample size is:
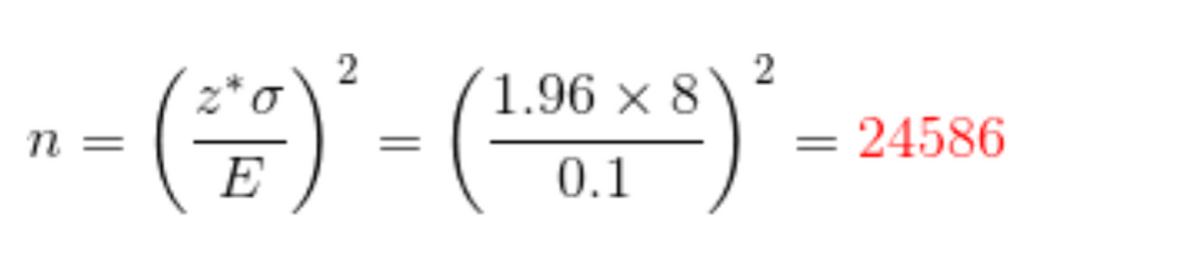
Step by step
Solved in 2 steps with 1 images









