style
Angles in Circles
Angles within a circle are feasible to create with the help of different properties of the circle such as radii, tangents, and chords. The radius is the distance from the center of the circle to the circumference of the circle. A tangent is a line made perpendicular to the radius through its endpoint placed on the circle as well as the line drawn at right angles to a tangent across the point of contact when the circle passes through the center of the circle. The chord is a line segment with its endpoints on the circle. A secant line or secant is the infinite extension of the chord.
Arcs in Circles
A circular arc is the arc of a circle formed by two distinct points. It is a section or segment of the circumference of a circle. A straight line passing through the center connecting the two distinct ends of the arc is termed a semi-circular arc.
![### Problem 13.
**Task:** Using the style laid out in class, verify the following identity:
\[ \cot^2\left(\frac{\alpha}{2}\right) = \frac{2 + 2 \cos(\alpha) - \sin^2(\alpha)}{\sin^2(\alpha)} \]
---
In the problem, you are required to verify the trigonometric identity given. The left side of the equation involves the square of the cotangent of \(\frac{\alpha}{2}\), while the right side involves a more complex expression with trigonometric functions of \(\alpha\).
Understanding trigonometric identities and their verification methods is crucial for solving this problem. Be sure to use the techniques and strategies discussed in class to approach and simplify both sides of the given equation.
Review your notes on double-angle and half-angle identities if needed, and ensure to show each step of your verification process clearly and logically.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F782aa8c0-fab4-4035-9c3e-0862db729267%2F60582e85-6cc5-41d8-80bd-9c74d5d74888%2Fhfuz9bi.jpeg&w=3840&q=75)
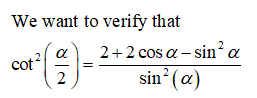
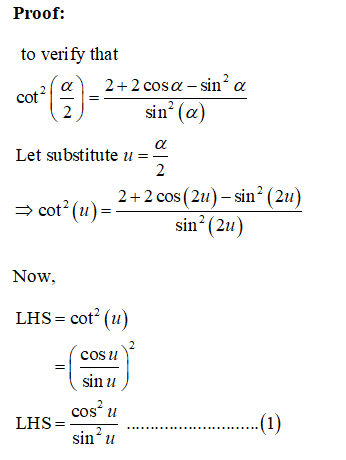
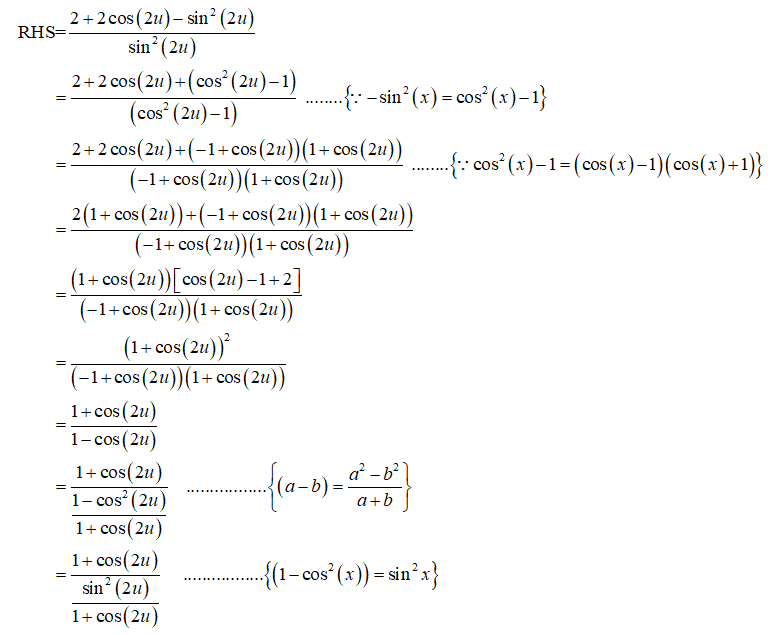

Hence verified
Step by step
Solved in 3 steps with 5 images







