Statistics Question

Solution:
Given:
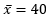
σ = 3 and n = 18
Confidence interval for µ is required.
Part a)
Population standard deviation (σ) is known, so Z confidence interval is used.
The formula of confidence interval for µ is:
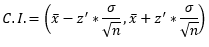
Steps to find critical z value (z'):
Confidence Level: C = 90% = 0.90
α=1-C
= 1- 0.90
α= 0.10
α/2= 0.10/2 = 0.05
1- (α/2) = 1-0.05 = 0.95
z' can be easily found using excel function, =NORMSINV(1-(α/2))
=NORMSINV(0.95) is 1.644854
Thus, z' = 1.644854
Substituting all the values in the formula of confidence interval, we get,

=(40 - 1.644854*0.707107, 40 + 1.644854*0.707107)
=(40 - 1.163087, 40 + 1.163087)
=(38.83691, 41.16309)
Rounding it to 4 decimal places, it becomes (38.8369, 41.1631).
The 90% confidence interval is from 38.8369 to 41.1631.
Part b)
Steps to find critical z value (z'):
Confidence Level: C = 95% = 0.95
α=1-C
= 1- 0.95
α= 0.05
α/2= 0.05/2 = 0.025
1- (α/2) = 1-0.025 = 0.975
z' can be easily found using excel function, =NORMSINV(1-(α/2))
=NORMSINV(0.975) is 1.959964
Thus, z' = 1.959964
Substituting all the values in the formula of confidence interval, we get,
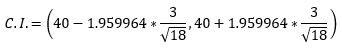
=(40 - 1.959964*0.707107, 40 + 1.959964*0.707107)
=(40 - 1.385904, 40 + 1.385904)
=(38.6141, 41.3859)
Rounding it to 4 decimal places, it becomes (38.6141, 41.3859).
The 95% confidence interval is from 38.6141 to 41.3859.
Step by step
Solved in 4 steps with 5 images









