State True or False, no justification needed. (a) The functions f₁ (t) = t and f2(t) = e²t are linearly independent on the interval (-1,1). (b) The functions g₁ (t) = 2 sin² t and g2 (t) = 1 − cos² t are linearly independent on the interval (-1,1).
State True or False, no justification needed. (a) The functions f₁ (t) = t and f2(t) = e²t are linearly independent on the interval (-1,1). (b) The functions g₁ (t) = 2 sin² t and g2 (t) = 1 − cos² t are linearly independent on the interval (-1,1).
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:State True or False, no justification needed.
(a) The functions f₁ (t) = t and f₂(t) = e²t are linearly independent on the interval
(-1,1).
(b) The functions g₁ (t) = 2 sin² t and g₂ (t) = 1 − cos² t are linearly independent
on the interval (−1,1).
(c) The function
x(t) = et - e-t
is a solution to the equation
(d) The function
x = x+e-t.
y(t) =
is a solution to the equation
-2
t² +1
y' = ty².
Expert Solution
NOTE:

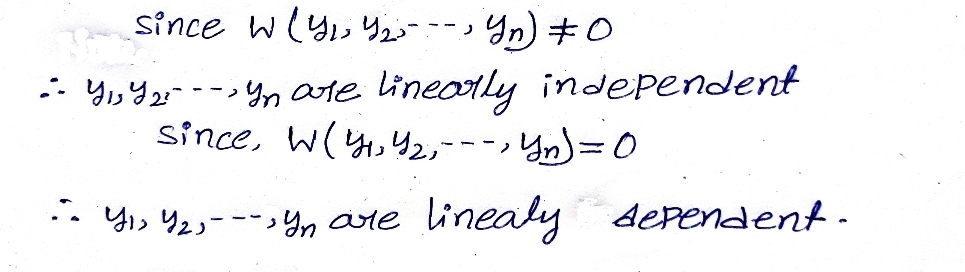
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

