Some of the balls are grey and some are white. The balls numbered 2 and 5 are grey. The balls numbered 1, 3, 4, and 6 are white. A ball will be selected from the bag at random.
Some of the balls are grey and some are white. The balls numbered 2 and 5 are grey. The balls numbered 1, 3, 4, and 6 are white. A ball will be selected from the bag at random.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%

Transcribed Image Text:Six balls numbered 1 to 6 are placed in a bag. Some of the balls are grey and some are white. The balls numbered 2 and 5 are grey. The balls numbered 1, 3, 4, and 6 are white.
A ball will be selected from the bag at random. The 6 possible outcomes are listed below. Note that each outcome has the same probability.
Visual Diagram:
- Number 1: white
- Number 2: grey
- Number 3: white
- Number 4: white
- Number 5: grey
- Number 6: white
Complete parts (a) through (c). Write the probabilities as fractions.
(a) Check the outcomes for each event below. Then, enter the probability of the event.
| Event | Description | Outcomes (1, 2, 3, 4, 5, 6) | Probability |
|-------|-------------|-----------------------------|-------------|
| Event A | The selected ball is white | □ □ □ □ □ □ | |
| Event B | The selected ball has an even number on it | □ □ □ □ □ □ | |
| Event A and B | The selected ball is white and has an even number on it | □ □ □ □ □ □ | |
| Event A or B | The selected ball is white or has an even number on it | □ □ □ □ □ □ | |
![### Probability Exercise Description
This exercise involves calculating probabilities based on different events related to selecting a ball from a set. The events are defined as follows:
- **Event B:** The selected ball has an even number on it.
- **Event A and B:** The selected ball is white *and* has an even number on it.
- **Event A or B:** The selected ball is white *or* has an even number on it.
### Task Instructions
1. **Compute the Following:**
The task is to solve the equation for the combined probabilities as given:
\[
P(A) + P(B) - P(A \text{ and } B) = \Box
\]
An empty box is provided for the answer.
2. **Select the Correct Answer:**
You need to choose the answer that makes the equation true:
\[
P(A) + P(B) - P(A \text{ and } B) = (\text{Choose one}) \, \Box
\]
A dropdown menu is given to select the appropriate value.
### Diagram Explanation
The diagram in this exercise consists of icons representing different configurations of the events. Checkboxes are provided to select or mark the condition that satisfies the event descriptions.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff996b914-e3a0-44c6-acc6-2ba9d8d3eb2a%2Fcd599973-9a90-44a0-9009-09599b76e820%2F9lb2gf8_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Probability Exercise Description
This exercise involves calculating probabilities based on different events related to selecting a ball from a set. The events are defined as follows:
- **Event B:** The selected ball has an even number on it.
- **Event A and B:** The selected ball is white *and* has an even number on it.
- **Event A or B:** The selected ball is white *or* has an even number on it.
### Task Instructions
1. **Compute the Following:**
The task is to solve the equation for the combined probabilities as given:
\[
P(A) + P(B) - P(A \text{ and } B) = \Box
\]
An empty box is provided for the answer.
2. **Select the Correct Answer:**
You need to choose the answer that makes the equation true:
\[
P(A) + P(B) - P(A \text{ and } B) = (\text{Choose one}) \, \Box
\]
A dropdown menu is given to select the appropriate value.
### Diagram Explanation
The diagram in this exercise consists of icons representing different configurations of the events. Checkboxes are provided to select or mark the condition that satisfies the event descriptions.
Expert Solution
Step 1
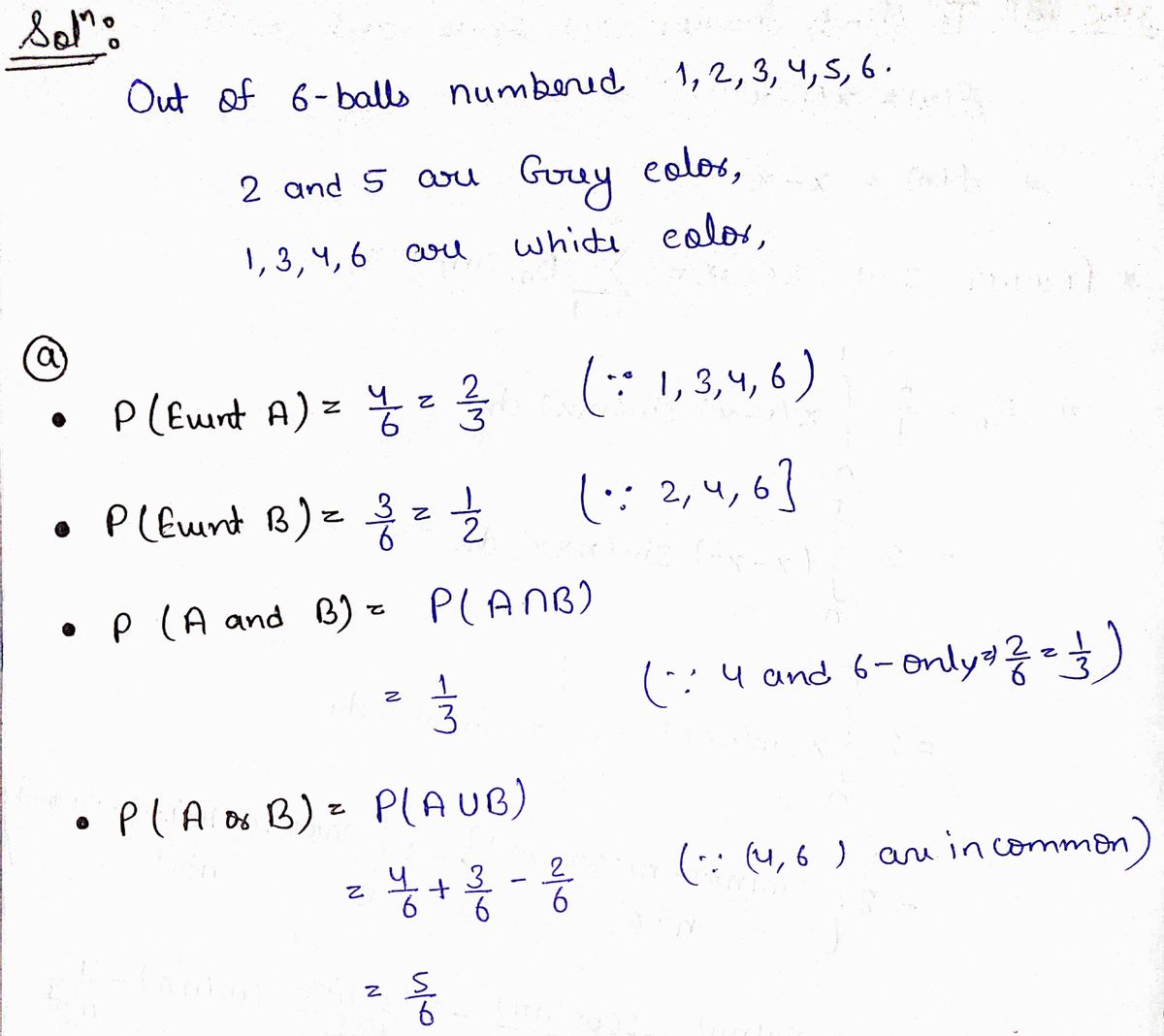
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

