Some colleges now aw students to pay their tution using a credit card. A report includes data from a survey of 100 public -year colleges, 100 private 4-year colleges, and 100 community colleges. The accompanying table gives information on credit card acceptance for each of these samples of colleges Does Not Accept Credit Cards for Tuition Payment Public 4-Year Colleges Private 4-Year Colleges Accepts t Cards for T Payment RS 43 100 15 31 Community Caltegeக for purposes of this exercise, suppose that these three samples are representative of the populations of public 6-year colleges private dar cueges 0 Since this problem wants to find of the proportion in each of the two credit card categories are not all the same for all three types of colleges, we must translate the question of interest to the Select the appropriate mult and aternative hypotheses The proportions fatting into each of the two credit card categories are the same for all three types of colleges The proportions falling into each of the two credit card categories are not the same for all three types of colleges The proportions talling into each of the two credit card categories are not different for all three types of colleges The proporttaling into each of the two credit card categories are different for all three types of colleges O The proportions tatting into each of the two credit card categories are different for all three types of colleges The proportions fating into each of the two credit card categories are not different for all three types of colleges OH The proportions falling to each of the two credit card categories are not the same for all three types of co The proportions falling into each of the two credit card categories are the same for all three types of o evidence that the proportions each of the two credit car categories are not the same for all three types of colleges? Test the releva 0.05 significance level (See Example 12.5)
Some colleges now aw students to pay their tution using a credit card. A report includes data from a survey of 100 public -year colleges, 100 private 4-year colleges, and 100 community colleges. The accompanying table gives information on credit card acceptance for each of these samples of colleges Does Not Accept Credit Cards for Tuition Payment Public 4-Year Colleges Private 4-Year Colleges Accepts t Cards for T Payment RS 43 100 15 31 Community Caltegeக for purposes of this exercise, suppose that these three samples are representative of the populations of public 6-year colleges private dar cueges 0 Since this problem wants to find of the proportion in each of the two credit card categories are not all the same for all three types of colleges, we must translate the question of interest to the Select the appropriate mult and aternative hypotheses The proportions fatting into each of the two credit card categories are the same for all three types of colleges The proportions falling into each of the two credit card categories are not the same for all three types of colleges The proportions talling into each of the two credit card categories are not different for all three types of colleges The proporttaling into each of the two credit card categories are different for all three types of colleges O The proportions tatting into each of the two credit card categories are different for all three types of colleges The proportions fating into each of the two credit card categories are not different for all three types of colleges OH The proportions falling to each of the two credit card categories are not the same for all three types of co The proportions falling into each of the two credit card categories are the same for all three types of o evidence that the proportions each of the two credit car categories are not the same for all three types of colleges? Test the releva 0.05 significance level (See Example 12.5)
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
helpp15

Transcribed Image Text:Tutorial Exercise
Some colleges now allow students to pay their tuition using a credit card. A report includes data from a survey of 100 public 4-year colleges, 100 private 4-year colleges, and 100 community colleges. The accompanying table gives information on credit card acceptance for each of these samples of colleges.
Public 4-Year
Colleges
Private 4-Year
Colleges
Community Colleges
Accepts Credit
Cards for Tuition
Payment
85
63
Submit Skip (you cannot come back)
100
Does Not Accept
Credit Cards for
Tuition Payment
37
0
For purposes of this exercise, suppose that these three samples are representative of the populations of public 4-year colleges, private 4-year colleges, and community colleges in the United States. Is there convincing evidence that the proportions in each of the two credit card categories are not the same for all three types of colleges? Test the relevant hypotheses using a 0.05 significance level. (Hint: See Example 12.5.)
Step 1
Since this problem wants to find if the proportion in each of the two credit card categories are not all the same for all three types of colleges, we must translate the question of interest into hypothesis.
Select the appropriate null and alternative hypotheses.
O H₂: The proportions falling into each of the two credit card categories are the same for all three types of colleges.
H₂: The proportions falling into each of the two credit card categories are not the same for all three types of colleges.
OH: The proportions falling into each of the two credit card categories are not different for all three types of colleges.
H₂: The proportions falling into each of the two credit card categories are different for all three types of colleges.
OH: The proportions falling into each of the two credit card categories are different for all three types of colleges.
H₂: The proportions falling into each of the two credit card categories are not different for all three types of colleges.
O H: The proportions falling into each of the two credit card categories are not the same for all three types of colleges.
H₂: The proportions falling into each of the two credit card categories are the same for all three types of colleges.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
15. help please. step 2 ty!
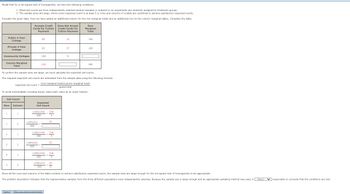
Transcribed Image Text:Recall that for a chi-square test of homogeneity, we have the following conditions.
1. Observed counts are from independently selected random samples or subjects in an experiment are randomly assigned to treatment groups.
2. The sample sizes are large, where every expected count is at least 5 or rows and columns of a table are combined to achieve satisfactory expected counts.
Consider the given data. Here we have added an additional column for the row marginal totals and an additional row for the column marginal tables. Complete the table.
Community Colleges
Column Marginal
Total
Private 4-Year
College
Cell Count
Row Column
1
Public 4-Year
College
1
2
2
3
3
1
2
1
2
To confirm the sample sizes are large, we must calculate the expected cell counts.
The required expected cell counts are estimated from the sample data using the following formula.
expected cell count = (row marginal total) (column marginal total)
grand total
To avoid intermediate rounding issues, leave each value as an exact fraction.
1
Accepts Credit
Cards for Tuition
Payment
2
85
(100)(52)
300
63
100
248
Expected
Cell Count
(100)(52)
300
(100)(248) 248
300
(100)(248)
300
300
(100) (248)
300
(100) (52)
S
52
Submit Skip (you cannot come back)
248
=
3
52
248
7
Does Not Accept
Credit Cards for
Tuition Payment
52
15
37
0
Row
Marginal
Total
100
100
300
Since all the rows and columns of the table combine to achieve satisfactory expected counts, the sample sizes are large enough for the chi-square test of homogeneity to be appropriate.
The problem description indicates that the representative samples from the three different populations were independently selected. Because the sample size is large enough and an appropriate sampling method was used, it -Select-reasonable to conclude that the conditions are met.
Solution
Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
