Solve (y - 3)² = -54 for y y=3± √6i y = 3±3i y=3±3√6i y = 3+ 6i
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem:**
Solve the equation \((y - 3)^2 = -54\) for \(y\).
**Answer Choices:**
- \(y = 3 \pm \sqrt{6}i\)
- \(y = 3 \pm 3i\)
- \(y = 3 \pm 3\sqrt{6}i\)
- \(y = 3 \pm 6i\)
**Solution Explanation:**
1. Start with the given equation: \((y - 3)^2 = -54\).
2. Take the square root of both sides:
\[
y - 3 = \pm \sqrt{-54}
\]
3. Recognize that \(\sqrt{-54}\) can be rewritten using imaginary numbers:
\[
\sqrt{-54} = \sqrt{54} \cdot i = \sqrt{9 \times 6} \cdot i = 3\sqrt{6} \cdot i
\]
4. Substituting back, we have:
\[
y - 3 = \pm 3\sqrt{6}i
\]
5. Solve for \(y\):
\[
y = 3 \pm 3\sqrt{6}i
\]
Thus, the correct answer is: \(y = 3 \pm 3\sqrt{6}i\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F67c02a1a-91b6-4dde-807f-4ee7d9512ede%2Fdca34478-e43a-47e9-b13a-e6b773052ce6%2Fxyibkxq_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem:**
Solve the equation \((y - 3)^2 = -54\) for \(y\).
**Answer Choices:**
- \(y = 3 \pm \sqrt{6}i\)
- \(y = 3 \pm 3i\)
- \(y = 3 \pm 3\sqrt{6}i\)
- \(y = 3 \pm 6i\)
**Solution Explanation:**
1. Start with the given equation: \((y - 3)^2 = -54\).
2. Take the square root of both sides:
\[
y - 3 = \pm \sqrt{-54}
\]
3. Recognize that \(\sqrt{-54}\) can be rewritten using imaginary numbers:
\[
\sqrt{-54} = \sqrt{54} \cdot i = \sqrt{9 \times 6} \cdot i = 3\sqrt{6} \cdot i
\]
4. Substituting back, we have:
\[
y - 3 = \pm 3\sqrt{6}i
\]
5. Solve for \(y\):
\[
y = 3 \pm 3\sqrt{6}i
\]
Thus, the correct answer is: \(y = 3 \pm 3\sqrt{6}i\).
Expert Solution
Step 1: Introduction of the problem
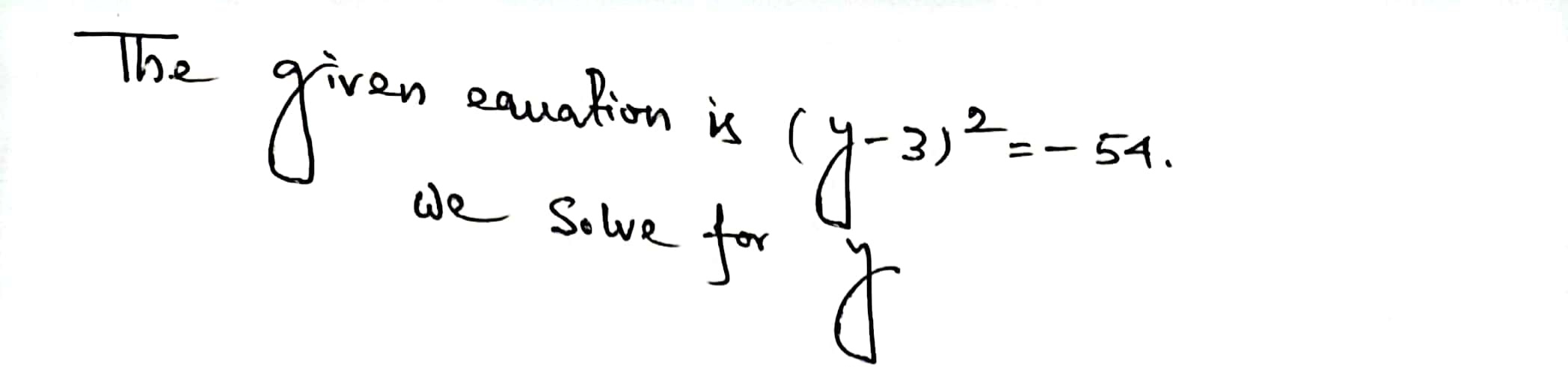
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

