Solve the linear programming problem using the simplex method. 9x + 2y ≤70 x+y≤60 x20, y 20 Maximize 2x +9y+ 300 subject to the constraints Find the solution. x= y = M = C
Solve the linear programming problem using the simplex method. 9x + 2y ≤70 x+y≤60 x20, y 20 Maximize 2x +9y+ 300 subject to the constraints Find the solution. x= y = M = C
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Linear Programming Problem Using the Simplex Method**
**Objective:**
Maximize the function \(2x + 9y + 300\)
**Subject to the Constraints:**
1. \(9x + 2y \leq 70\)
2. \(x + y \leq 60\)
3. \(x \geq 0, y \geq 0\)
**Steps to Solve the Problem:**
1. **Identify the Objective Function:**
- The objective is to maximize \(2x + 9y + 300\).
2. **Understand the Constraints:**
- The inequalities \(9x + 2y \leq 70\) and \(x + y \leq 60\) are the constraints that define the feasible region.
- The constraints \(x \geq 0\) and \(y \geq 0\) ensure that the solutions are non-negative.
3. **Graphical Representation (if applicable):**
- Although not detailed here, typically you'd draw the lines for each constraint on a graph to identify the feasible region.
- The intersection points of the lines and the axes would be calculated to explore potential optimal solutions.
4. **Simplex Method Application:**
- Formulate the problem for the simplex algorithm.
- Identify the basic feasible solutions.
- Execute iterations of the simplex method to move towards the optimal point within the feasible region.
**Find the Solution:**
- Determine the optimal values for:
- \(x = \) [ ]
- \(y = \) [ ]
- Maximum value \(M = \) [ ]
Fill in the blanks with the values obtained through solving via the simplex method.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4726056b-a0d8-4167-a534-8f03670a441a%2F913a5ef8-26c2-40d5-b368-537014b2c142%2Fm1yr28r.png&w=3840&q=75)
Transcribed Image Text:**Linear Programming Problem Using the Simplex Method**
**Objective:**
Maximize the function \(2x + 9y + 300\)
**Subject to the Constraints:**
1. \(9x + 2y \leq 70\)
2. \(x + y \leq 60\)
3. \(x \geq 0, y \geq 0\)
**Steps to Solve the Problem:**
1. **Identify the Objective Function:**
- The objective is to maximize \(2x + 9y + 300\).
2. **Understand the Constraints:**
- The inequalities \(9x + 2y \leq 70\) and \(x + y \leq 60\) are the constraints that define the feasible region.
- The constraints \(x \geq 0\) and \(y \geq 0\) ensure that the solutions are non-negative.
3. **Graphical Representation (if applicable):**
- Although not detailed here, typically you'd draw the lines for each constraint on a graph to identify the feasible region.
- The intersection points of the lines and the axes would be calculated to explore potential optimal solutions.
4. **Simplex Method Application:**
- Formulate the problem for the simplex algorithm.
- Identify the basic feasible solutions.
- Execute iterations of the simplex method to move towards the optimal point within the feasible region.
**Find the Solution:**
- Determine the optimal values for:
- \(x = \) [ ]
- \(y = \) [ ]
- Maximum value \(M = \) [ ]
Fill in the blanks with the values obtained through solving via the simplex method.
Expert Solution
Step 1: Introduction to the question
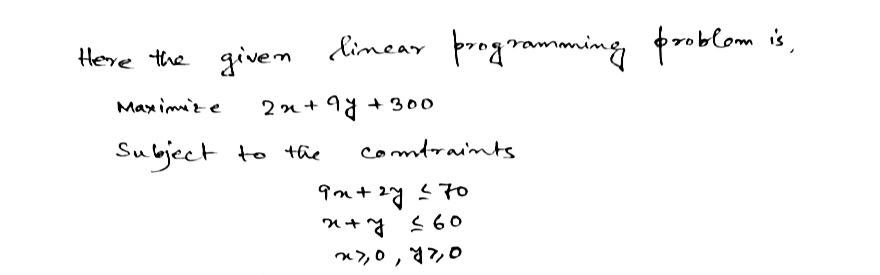
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

